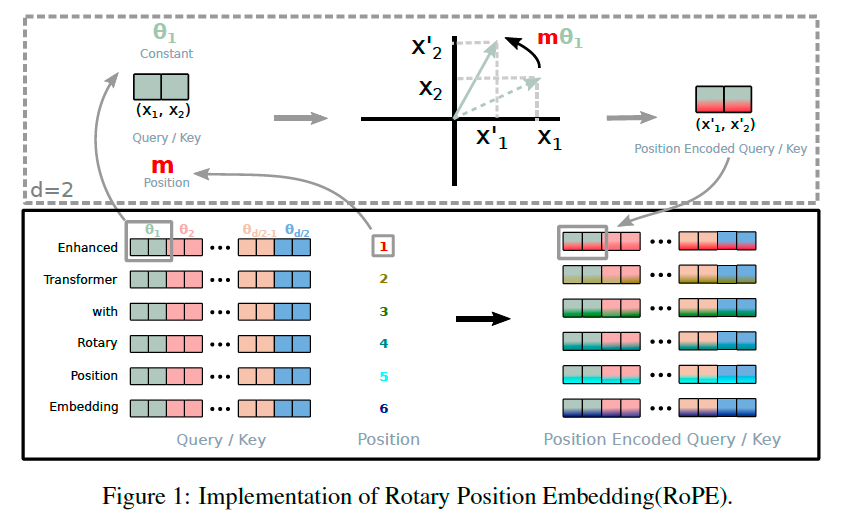
RoPE

Note

Transformer-based language modeling usually leverages the position information of individual tokens through a self-attention mechanism. \(\mathbf{q}_{m}^{\intercal}\mathbf{k}_{n}\) typically enables knowledge transfer between tokens at different positions. In order to incorporate relative position information, we require the inner product of query \(\mathbf{q}_{m}\) and key \(\mathbf{k}_{n}\) to be formulated by a function \(g\), which takes only the word embeddings \(\mathbf{x}_{m}\), \(\mathbf{x}_{n}\), and their relative position \(m-n\) as input variables.

\[f_{q}(\mathbf{x}_{m}, m)^{\intercal}f_{k}(\mathbf{x}_{n}, n) = g(\mathbf{x}_{m}, \mathbf{x}_{n}, m-n)\]

2D case

Begin with \(d=2\), we make use of the property of the rotary matrix:

\[\begin{split} \begin{aligned} \mathbf{R}_{m\theta} &= \begin{pmatrix} \cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{pmatrix}\\ \mathbf{R}_{m\theta}^{\intercal} &= \mathbf{R}_{-m\theta}\\ \mathbf{R}_{m\theta}\mathbf{R}_{n\theta} &= \mathbf{R}_{(m+n)\theta} \end{aligned} \end{split}\]

Let:

\[\begin{split} \begin{aligned} f_{q}(\mathbf{x}_{m}, m) &= \mathbf{R}_{m\theta}\mathbf{W}_{q}\mathbf{x}_{m}\\ f_{k}(\mathbf{x}_{n}, n) &= \mathbf{R}_{n\theta}\mathbf{W}_{k}\mathbf{x}_{n} \end{aligned} \end{split}\]

Then:

\[\begin{split} \begin{aligned} f_{q}(\mathbf{x}_{m}, m)^{\intercal}f_{k}(\mathbf{x}_{n}, n) &= (\mathbf{R}_{m\theta}\mathbf{W}_{q}\mathbf{x}_{m})^{\intercal}\mathbf{R}_{n\theta}\mathbf{W}_{k}\mathbf{x}_{n} \\ &= (\mathbf{W}_{q}\mathbf{x}_{m})^{\intercal}\mathbf{R}_{(n-m)\theta}(\mathbf{W}_{k}\mathbf{x}_{n}) \end{aligned} \end{split}\]

Tip

\( \mathbf{R}_{\theta}\mathbf{v}\) equals counterclockwise rotation of \(\mathbf{v}\) through angle \(\theta\).

General form

In order to generalize our results in 2D to any \(\mathbf{x}_{i}\in\mathbb{R}^{d}\) where \(d\) is even, we divide the d-dimensional space into \(d/2\) sub-spaces:

\[\begin{split} R_{m,\Theta}^{d} = \begin{pmatrix} \cos m\theta_{1} & -\sin m\theta_{1} & 0 & 0 & \dots & 0 & 0 \\ \sin m\theta_{1} & \cos m\theta_{1} & 0 & 0 & \dots & 0 & 0\\ 0 & 0 & \cos m\theta_{2} & -\sin m\theta_{2} & \dots & 0 & 0\\ 0 & 0 & \sin m\theta_{2} & \cos m\theta_{2} & \dots & 0 & 0\\ \vdots& \vdots& \vdots& \vdots& \ddots &\vdots &\vdots \\ 0& 0& 0& 0& \dots& \cos m\theta_{d/2} & -\sin m\theta_{d/2} \\ 0& 0& 0& 0& \dots& \sin m\theta_{d/2} & \cos m\theta_{d/2} \end{pmatrix} \end{split}\]

is the rotary matrix with pre-defined parameters \(\Theta = \{\theta_{i}=10000^{-2(i-1)/d},i\in[1,2,\dots,d/2]\}\). RoPE encodes the absolute position with a rotation matrix and meanwhile incorporates the explicit relative position dependency in self-attention formulation.

Tip

\[1 = \theta_{1} > \theta_{2} > \dots > \theta_{d/2} \approx \frac{1}{10000}\]

where 10000 is the RoPE base, \(\theta_{1}\) corresponds to the highest frequency. Smaller \(i\) encodes high frequency information (information nearby).