DeepSeekMoE

Note

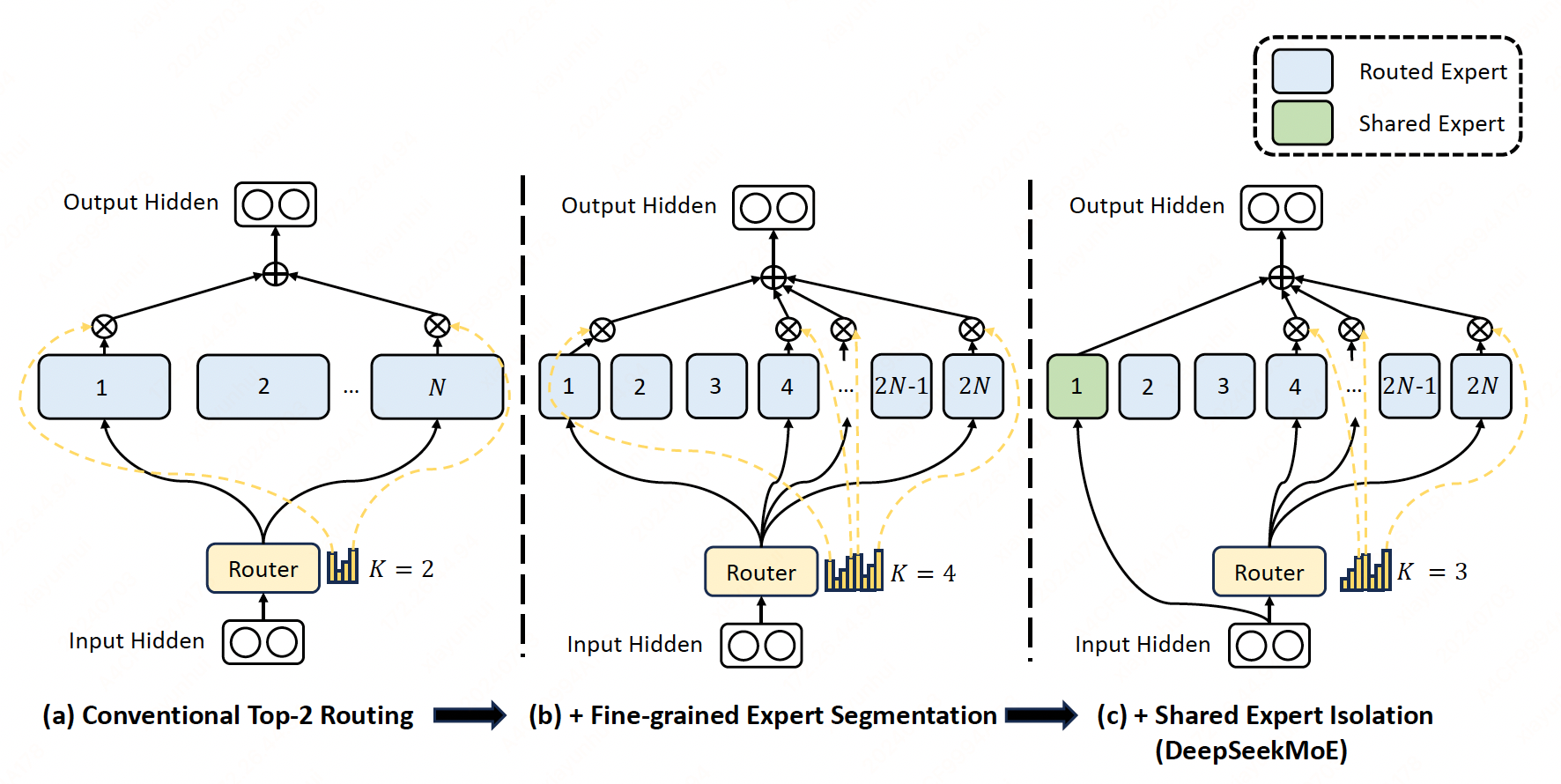
We propose the DeepSeekMoE architecture towards ultimate expert specialization. It involves two principal strategies:

1. Finely segmenting the experts into \(mN\) ones and activating \(mK\) from them, allowing for a more flexible combination of activated experts.
   

2. Isolating \(K_s\) experts as shared ones, aiming at capturing common knowledge and mitigating redundancy in routed experts.

Preliminaries: Mixture-of-Experts for Transformers

A standard Transformer language model is constructed by stacking \(L\) layers of standard Transformer blocks, where each block can be represented as follows:

\[\begin{split} \begin{aligned} \mathbf{u}_{1:T}^{l} &= \text{Self-Att}(\mathbf{h}_{1:T}^{l-1}) + \mathbf{h}_{1:T}^{l-1}\\ \mathbf{h}_{t}^{l} &= \text{FFN}(\mathbf{u}_{t}^{l}) + \mathbf{u}_{t}^{l} \end{aligned} \end{split}\]

where \(T\) denotes the sequence length, \(\text{Self-Att}(·)\) denotes the self-attention module, \(\text{FFN}(·)\) denotes the Feed-Forward Network (FFN), \(\mathbf{u}_{1:T}^{l}\in\mathbb{R}^{T\times d}\) are the hidden states of all tokens after the \(l\)-th attention module, and \(\mathbf{h}_{t}^{l}\in\mathbb{R}^{d}\) is the output hidden state of the \(t\)-th token after the \(l\)-th Transformer block. We omit the layer normalization in the above formulations for brevity.

A typical practice to construct an MoE language model usually substitutes FFNs in a Transformer with MoE layers. An MoE layer is composed of multiple experts, where each expert is structurally identical to a standard FFN. Then, each token will be assigned to one or two experts. If the \(l\)-th FFN is substituted with an MoE layer:

\[\begin{split} \begin{aligned} \mathbf{h}_{t}^{l} &= \sum_{i=1}^{N}(g_{i,t}\text{FFN}_{i}(\mathbf{u_{t}^{l}})) + \mathbf{u}_{t}^{l}\\ g_{i,t} &= \begin{cases} s_{i,t},\quad &s_{i,t}\in\text{Topk}(\{s_{j,t}|1\le j\le N\}, K)\\ 0, &\text{otherwise} \end{cases}\\ s_{i,t} &= \text{Softmax}_{i}({\mathbf{u}_{t}^{l}}^{\intercal}\mathbf{e}_{i}^{l}) \end{aligned} \end{split}\]

where \(N\) denotes the total number of experts, \(\text{FFN}_{i}\) is the \(i\)-th expert FFN, \(g_{i,t}\) denotes the gate value for the \(i\)-th expert, \(s_{i,t}\) denotes the token-to-expert affinity, \(\text{Topk}(\cdot,K)\) denotes the set comprising \(K\) highest affinity scores among those calculated for the \(t\)-th token and all \(N\) experts, and \(\mathbf{e}_{i}^{l}\) is the parameter of the gate.

Fine-Grained Expert Segmentation

The finer expert segmentation enables a more flexible and adaptable combination of activated experts.

Shared Expert Isolation

Tokens assigned to different experts may necessitate some common knowledge or information. So in addition to the fine-grained expert segmentation strategy, we further isolate \(K_{s}\) experts to serve as shared experts.

Load Balance Consideration

Automatically learned routing strategies may encounter the issue of load imbalance.

Expert-Level Balance Loss

Imbalance leeds to higher loss.

\[\begin{split} \begin{aligned} \mathcal{L}_{\text{ExpBal}} &= \alpha_{1}\sum_{i=1}^{mN-K_s}f_{i}P_{i}\\ f_{i} &= \frac{mN-K_{s}}{(mK-K_s)T}\sum_{t=1}^{T}\mathbb{1}(\text{Token }t\text{ selects Expert }i)\\ P_{i} &= \frac{1}{T}\sum_{t=1}^{T}s_{i,t} \end{aligned} \end{split}\]

• \(f_{i}\): normalized frequency of the \(i\)-th expert, \(\sum_{i=1}^{N'}f_{i}=N'\).

• \(P_{i}\): normalized weight of the \(i\)-th expert, \(\sum_{i=1}^{N'}P_{i}=N'\).

Tip

For DeepSeek-V2, beyond the naive top-\(K\) selection of routed experts, we additionally ensure that the target experts of each token will be distributed on at most \(M\) devices.

Device-Level Balance Loss

In addition to the expert-level balance loss, we additionally design a device-level balance loss to ensure balanced computation across different devices. If we partition all routed experts into \(D\) groups \(\{\mathcal{E}_{1}, \mathcal{E}_{2}, \dots, \mathcal{E}_{D}\}\), and deploy each group on a single device, the device-level balance loss is computed as follows:

\[\begin{split} \begin{aligned} \mathcal{L}_{\text{DevBal}} &= \alpha_{2}\sum_{i=1}^{D}f_{i}'P_{i}'\\ f_{i}' &= \frac{1}{|\mathcal{E}_{i}|}\sum_{j\in\mathcal{E}_{i}}f_{j}\\ P_{i}' &= \sum_{j\in\mathcal{E}_{i}}P_{j} \end{aligned} \end{split}\]

Communication Balance Loss

Introduced in DeepSeek-V2[DALF+24].

When expert parallelism is employed, the routed experts will be distributed across multiple devices. For each token, its MoE-related communication frequency is proportional to the number of devices covered by its target experts. We introduce a communication balance loss to ensure that the communication of each device is balanced:

\[\begin{split} \begin{aligned} \mathcal{L}_{\text{CommBal}} &= \alpha_{3}\sum_{i=1}^{D}f_{i}''P_{i}''\\ f_{i}'' &= \frac{D}{MT}\sum_{t=1}^{T}\mathbb{1}(\text{Token }t\text{ is sent to Device }i)\\ P_{i}'' &= \sum_{j\in\mathcal{E}_{i}}P_{j} \end{aligned} \end{split}\]

Tip

Suppose expert1 and expert2 are in device1, expert3 and expert4 are in device2. Think about two situations:

1. token1 selects expert1 and expert2, token2 selects expert3 and expert4.

2. token1 selects expert1 and expert3, token2 selects expert2 and expert4.

They have the same device-Level Balance, but different communication balance.

Token-Dropping Strategy

In order to further mitigate the computation wastage caused by unbalanced load, we introduce a device-level token-dropping strategy during training.

This approach first computes the average computational budget for each device, which means that the capacity factor for each device is equivalent to 1.0. Then, we drop tokens with the lowest affinity scores on each device until reaching the computational budget (\(\le 1.0\)). In addition, we ensure that the tokens belonging to approximately 10% of the training sequences will never be dropped. In this way, we can flexibly decide whether to drop tokens during inference according to the efficiency requirements, and always ensure consistency between training and inference.