DAPO

Note

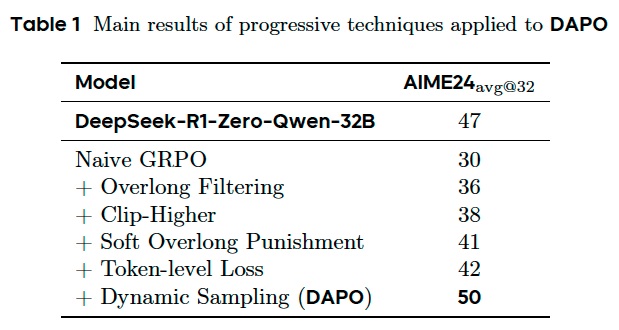
We propose the Decoupled Clip and Dynamic sAmpling Policy Optimization (DAPO) algorithm, and fully open-source a state-of-the-art large-scale RL system that achieves 50 points on AIME 2024 using Qwen2.5-32B base model.

Preliminary

PPO

GRPO

Removing KL Divergence

The KL penalty term is used to regulate the divergence between the online policy and the frozen reference policy. In the RLHF scenario, the goal of RL is to align the model behavior without diverging too far from the initial model. However, during training the long-CoT reasoning model, the model distribution can diverge significantly from the initial model, thus this restriction is not necessary. Therefore, we will exclude the KL term from our proposed algorithm.

Rule-based Reward Modeling

The use of reward model usually suffers from the reward hacking problem. Instead, we directly use the final accuracy of a verifiable task as the outcome reward:

\[\begin{split} R(\hat{y},y) = \begin{cases} 1,\quad &\text{isEquivalent}(\hat{y},y)\\ -1,&\text{otherwise} \end{cases} \end{split}\]

Tip

Reward hacking is when an AI system finds unexpected ways to maximize its reward function without achieving the intended goal.

DAPO

DAPO samples a group of outputs \(\{o_i\}_{i=1}^{G}\) for each question \(q\) paired with the answer \(a\) (ground truth), and optimizes the policy via the following objective:

\[\begin{split} \begin{aligned} \mathcal{J}_{\text{DAPO}}(\theta) = &\mathbb{E}_{(q,a)\sim\mathcal{D},\{o_i\}_{i=1}^{G}\sim \pi_{\theta_{\text{old}}}(\cdot|q)}\\ &\left[\frac{1}{\sum_{i=1}^{G}|o_i|}\sum_{i=1}^{G}\sum_{t=1}^{|o_i|}\min\left(r_{i,t}(\theta)\hat{A}_{i,t},\text{clip}(r_{i,t}(\theta), 1-\epsilon_{\text{low}}, 1+\epsilon_{\text{high}})\hat{A}_{i,t}\right)\right]\\ \text{s.t.}\quad&0<\left|\{o_i|\text{isEquivalent}(a,o_i)\}\right|<G \end{aligned} \end{split}\]

where

\[ r_{i,t}(\theta) = \frac{\pi_{\theta}(o_{i,t}|q, o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t}|q, o_{i,<t})},\quad\hat{A}_{i,t} = \frac{R_i -\text{mean}(\{R_i\})_{i=1}^{G}}{\text{std}(\{R_i\})_{i=1}^{G})} \]

In this section, we will introduce the key techniques associated with DAPO.

Clip-Higher

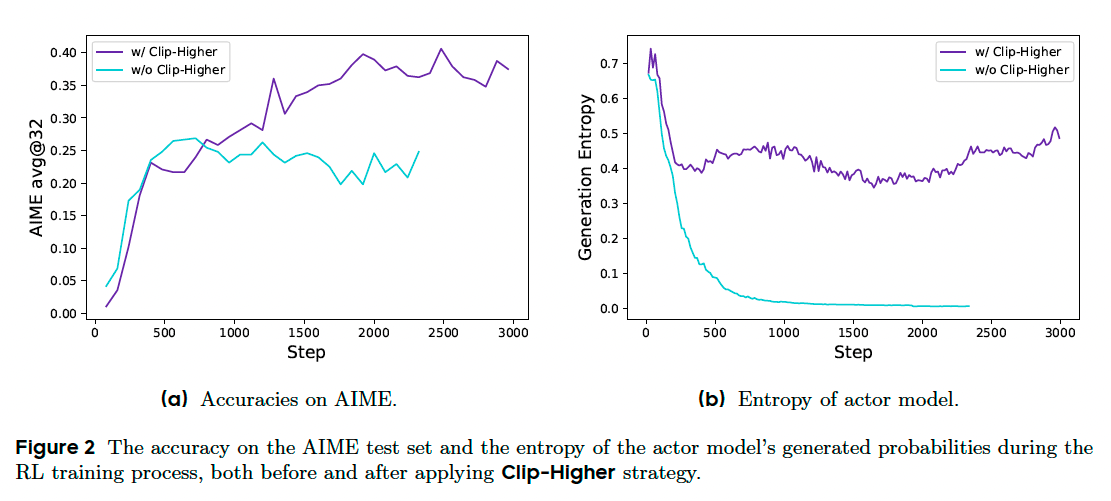
In our initial experiments using naive PPO or GRPO, we observed the entropy collapse phenomenon: the entropy of the policy decreases quickly as training progresses. The sampled responses of certain groups tend to be nearly identical.

We identify that the upper clip can restrict the exploration of the policy. In this case, it is much easier to make an ‘exploitation token’ more probable, than to uplift the probability of an unlikely ‘exploration token’. Concretely, when \(\epsilon=0.2\), consider two actions with probabilities \(\pi_{\theta_{\text{old}}}(o_i|q)=0.01\) and \(0.9\). The maximum possible updated probabilities \(\pi_{\theta_{\text{old}}}(o_i|q)=0.012\) and \(1.08\), respectively. This implies that for tokens with a higher probability (e.g., \(0.9\)) is less constrained. Conversely, for low-probability tokens, achieving a non-trivial increase in probability is considerably more challenging.

Adhering to the Clip-Higher strategy, we decouple the lower and higher clipping range as \(\epsilon_{\text{low}}\) and \(\epsilon_{\text{high}}\).

Dynamic Sampling

We propose to over-sample and filter out prompts with the accuracy equal to 1 and 0, leaving all prompts in the batch with effective gradients and keeping a consistent number of prompts. Besides, we find that with dynamic sampling the experiment achieves the same performance faster.

Token-Level Policy Gradient Loss

In the original GRPO algorithm, all samples are assigned the same weight in the loss calculation, tokens within longer responses (which contain more tokens) may have a disproportionately lower contribution to the overall loss, which can lead to:

1. For high-quality long samples, this effect can impede the model’s ability to learn reasoning-relevant patterns within them.

2. We observe that excessively long samples often exhibit low-quality patterns such as gibberish and repetitive words.

We introduce a Token-level Policy Gradient Loss in the long-CoT RL scenario to address the above limitations. In this setting, longer sequences can have more influence on the overall gradient update compared to shorter sequences. Moreover, from the perspective of individual tokens, if a particular generation pattern can lead to an increase or decrease in reward, it will be equally prompted or suppressed, regardless of the length of the response in which it appears.

Overlong Reward Shaping

In RL training, we typically set a maximum length for generation, with overlong samples truncated accordingly. By default, we assign a punitive reward to truncated samples. This approach may introduce noise into the training process, as a sound reasoning process can be penalized solely due to its excessive length. Such penalties can potentially confuse the model regarding the validity of its reasoning process.

To investigate the impact of this reward noise, we first apply an Overlong Filtering strategy which masks the loss of truncated samples. We find that this approach significantly stabilizes training and enhances performance.

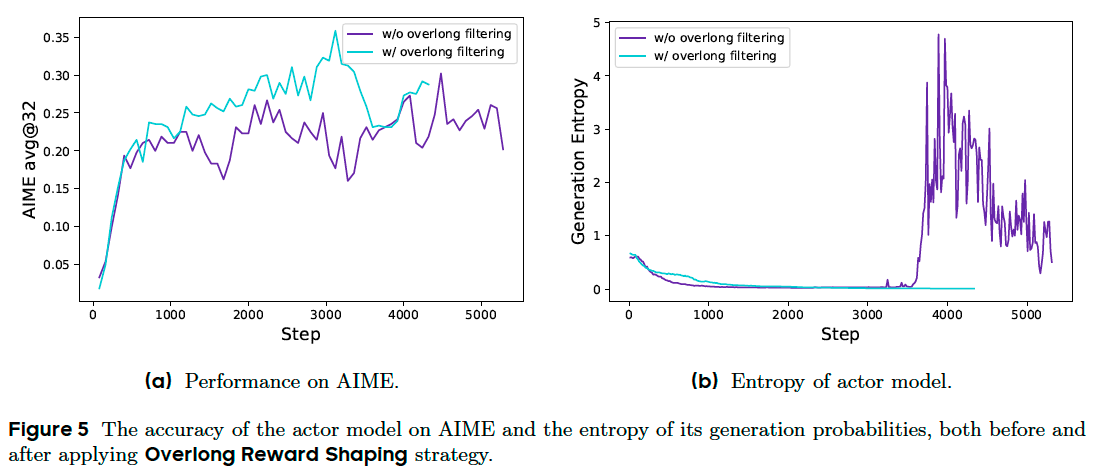
Furthermore, we propose Soft Overlong Punishment, this penalty is added to the original rule-based correctness reward, thereby signaling to the model to avoid excessively long responses.

\[\begin{split} R_{\text{length}}(y) = \begin{cases} 0, &|y|\le L_{\text{max}} - L_{\text{cache}}\\ \frac{(L_{\text{max}} - L_{\text{cache}}) - |y|}{L_{\text{cache}}},\ &L_{\text{max}} - L_{\text{cache}} < |y| \le L_{\text{max}}\\ -1, &L_{\text{max}}< |y|\\ \end{cases} \end{split}\]

Experiments

Dataset

Our dataset is sourced from the AoPS website and official competition homepages through a combination of web scraping and manual annotation. After selection and transformation, we obtained the DAPO-Math-17K dataset, which consists of 17K prompts, each paired with an integer as the answer.

Training Details

We use naive GRPO as our baseline algorithm.

For hyper-parameters, we utilize the AdamW ptimizer with a constant learning rate of \(1 × 10^{−6}\), incorporating a linear warm-up over 20 rollout steps. For rollout, the prompt batch size is 512 and we sample 16 responses for each prompt. For training, the mini-batch size is set to 512, i.e., 16 gradient updates for each rollout step. For Overlong Reward Shaping, we set the expected maximum length as 16,384 tokens and allocate additional 4,096 tokens as the soft punish cache. As for the Clip-Higher mechanism, we set the clipping parameter \(\epsilon_{\text{low}}\) to 0.2 and \(\epsilon_{\text{high}}\) to 0.28, which effectively balance the trade-off between exploration and exploitation. For evaluation on AIME, we repeat the evaluation set for 32 times and report avg@32 for results stability. The inference hyperparameters of evaluation are set to temperature 1.0 and topp 0.7.

Main Results

Experiments on AIME 2024 demonstrate that DAPO has successfully trained the Qwen-32B Base model into a powerful reasoning model, achieving performance superior to DeepSeek’s experiments on Qwen2.5-32B using the R1 approach.