AdaptiveStep

Note

We propose AdaptiveStep, a method that divides reasoning steps based on the model’s confidence in predicting the next word, our method requires no manual annotation.
Experiments with AdaptiveStep-trained PRMs in mathematical reasoning and code generation show that the outcome PRM achieves state-of-the-art Best-of-N performance, surpassing greedy search strategy with token-level value-guided decoding

AdaptiveStep

Given a question \(q \in Q\), we can generate \(N\) responses with temperature-based random sampling using the language model \(\pi\). We denote generated responses as \(\{s_1, s_2, \dots , s_N\}\).

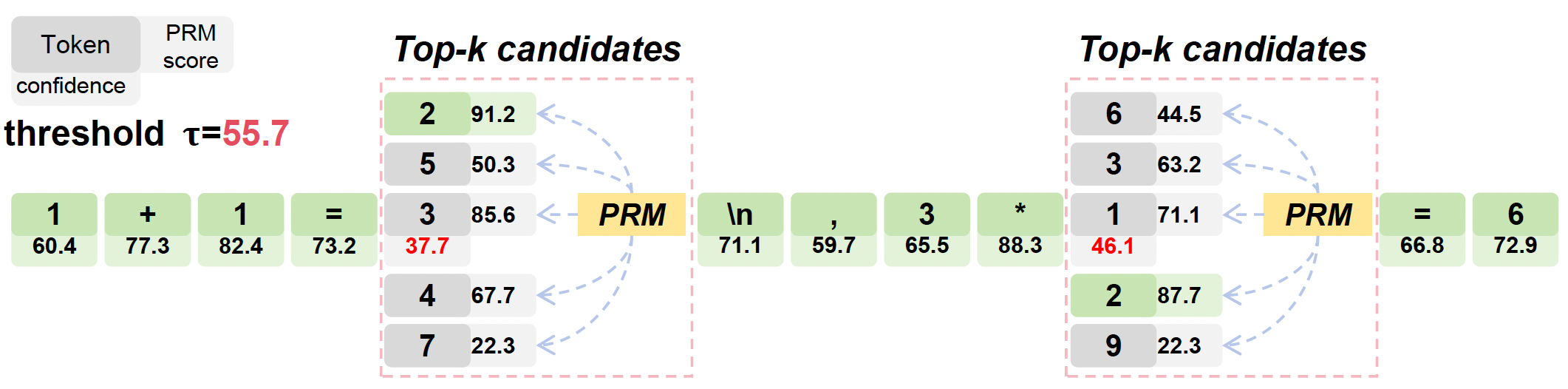
To divide the responses into reasoning steps, we use the probability of the sampled token as the metric for model confidence, and we determine a threshold \(\tau\).

Specifically, the model confidence can be written as

\[ c_{s_{i}^{n}} = p(s_{i}^{n}|\pi,q,s_{<i}^{n}) \]

where we use \(s_{i}^{n}\) and \(s_{<i}^{n}\) to denote the \(i\)-th token and the tokens prior to the \(i\)-th token in the response, respectively. Low model confidence at the \(i\)-th token indicates that the model is hard to determine the token selection at the ith position, and therefore, this position may become the starting point of a new reasoning step. According to the above procedure, we divide the response \(s_n\) into \(K\) reasoning steps \(s_n = \{r_1, r_2, \dots, r_K\}\).

PRM Training

To train a PRM based on the question-response pairs with divided reasoning steps, we first need to estimate the target reward for each reasoning step. We rollout the response generation process \(J\) times starting from each reasoning step, resulting in rollouts denoted as \(\{p, r_1, \dots, r_k, t_j\}_{k\in[K],j\in[J]}\), where \(t_j\) is the \(j\)-th trajectory starting from a partial response.

We use hard estimation (HE) to estimate the reward for the step \(r_k\). HE indicates whether any of the responses starting from the current partial response can reach a correct answer. Formally, the target reward can be estimated as:

\[\begin{split} r_{k}^{e} = \begin{cases} 1,\quad&\exists j\in[J],\{r_1,\dots,r_{k},t_j\}\text{ is correct}\\ 0,&\text{otherwise} \end{cases} \end{split}\]

With the target rewards estimated based on the rollouts, we can train PRM using the following loss:

\[ \mathcal{L}_{PRM}^{\theta} = -\sum_{k=1}^{K}(r_{k}^{e}\log r_{k}^{\theta} + (1 - r_{k}^{e})\log(1-r_{k}^{\theta})) \]

where \(r_{k}^{e}\) is the target reward and \(r_{k}^{\theta}:= R_{\theta}(p, r_1, \dots , r_k)\) denotes the reward predicted by the PRM \(R_{\theta}\).

Token-level Value-guided Decoding

The TVD strategy leverages the PRM to guide token selection during language model decoding. Specifically, when the model encounters a low confidence score (Top-1 probability \(c_p < \tau\) ) in decoding, it triggers the PRM to evaluate the tokens associated with the highest \(M\) probability given by the policy model \(\pi: \mathbf{s_{i}^{\ast}} = \{s_{i}^{1}, s_{i}^{2}, \dots, s_{i}^{M}\}\).

Among these candidates, the PRM selects the token it considers the best based on its learned reward estimation:

\[ s_{i} = \arg\underset{s_{i}^{m}\in\mathbf{s_{i}^{\ast}}}{\max}R^{\theta}(p,s_{<i},s_{i}^{m}). \]