West-of-N

Note

\(\text{Best-of-N} + \text{Worst-of-N} = \text{West-of-N}\)

Related Work

Best-of-N Sampling. Best-of-N, or rejection sampling is typically implemented by taking the top-scored generation within a pool of \(N\) candidates. In practice, Best-of-N strategies steer the output distribution towards high-reward generations, which has been shown to improve the performance of language models trained with supervised finetuning.

Synthetic Preference Data. Human preference data collection remains expensive, time-consuming and noisy; this motivates the use of synthetic data. RL from AI Feedback (RLAIF), is to use large language models to label response pairs instead of relying on human labeling. RL from Contrast Distillation (RLCD) use contrasting positive and negative prompts to produce pairs of high- and low-quality responses.

Self-Training for Preference Modeling

Assume access to some initial preference dataset \(\mathcal{D}_{L} = \{(x,y_{+},y_{-}):y_{+}\succ y_{-}\}\), which could consist of human preferences or other synthetically-generated data. We use this data to train a base preference model parameterized by \(\theta\): let \(P_{\theta}(y_{+}\succ y_{-}|x)\) model the probability of response \(y_{+}\) being preferred over \(y_{-}\) for a query \(x\).

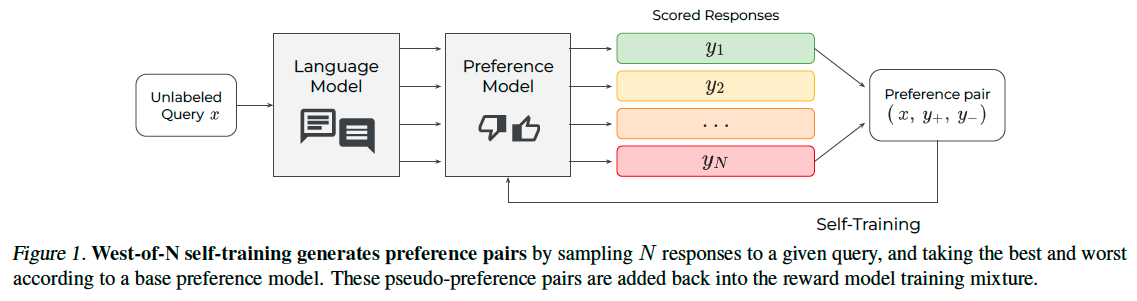
A simple strategy to generate synthetic preference data for unlabeled query \(x\) is to sample two responses \(y_{1}\), \(y_{2}\) from the generation policy \(\pi_{x}\), and to pseudo-label the preference pair based on \(P_{\theta}(y_1\succ y_2|x)\):

\[\begin{split} f_{\pm}(x) = \begin{cases} (y_1, y_2)\quad&\text{if}\quad P_{\theta}(y_1\succ y_2|x)>0.5\\ (y_2, y_1)&\text{else.} \end{cases} \end{split}\]

RL from AI Feedback can be seen as an example of this approach. In this special case, \(\mathcal{D}_{L}=\emptyset\) and pseudolabeling is achieved through few-shot prompting.

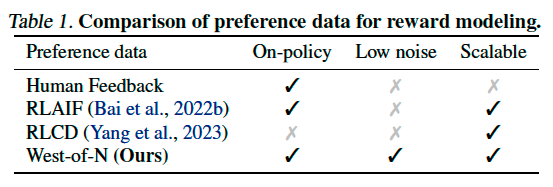
West-of-N Self-Training

As in any self-training effort, the above pseudolabeling approach is highly dependent on the performance of base model \(P_{\theta}\): an imperfect model will often assign incorrect labels to preference pairs. This is mitigated in prior self-training work by only retaining samples with highconfidence pseudolabels

Extending this idea, we propose to maximize the probability of correctly labeling a pair of on-policy responses to a given query, according to the base preference model:

\[ \underset{(y_{+},y_{-})\sim\pi(x)}{\max}P_{\theta}(y_+\succ y_-|x) \]

In practice, this objective can be approximated by sampling a pool of \(N\) candidate outputs from the policy and identify the best- and worst-scored ones.

Tip

Pseudo-Preference Filtering. To further improve the quality of generated preference pairs, these can be filtered based on the confidence of their preference label and their coverage of the relevant response distribution.

We measure model confidence in labeling a preference through the prediction \(P_{\theta}(y_+\succ y_-|x)\), and only retain West-of-N pairs above a certain quantile. Similarly, we also apply a likelihood threshold of both positive and negative responses \(\pi(y_{+}|x)\) and \(\pi(y_{-}|x)\), to ensure the responses being compared remain in-distribution. We determine final threshold values through validation performance.