Multi-Head Latent Attention

Note

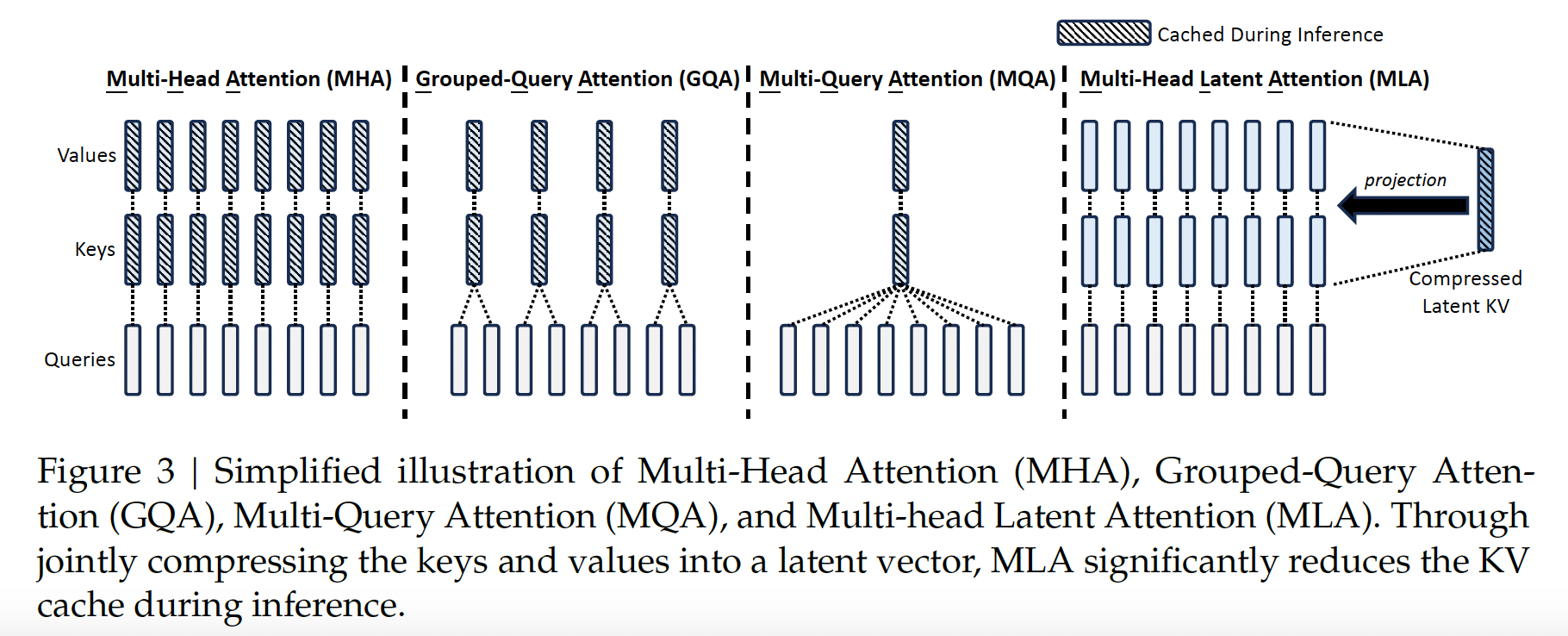
Conventional Transformer models usually adopts Multi-Head Attention (MHA)[VSP+23], but during generation, its heavy Key-Value (KV) cache will become the bottleneck that limit the inference efficiency. In order to reduce the KV cache, Multi-Query Attention (MQA). and Grouped-Query Attention (GQA) are proposed. They require a smaller magnitude of KV cache, but their performance does not match MHA.

For DeepSeek-V2, we design an innovative attention mechanism called Multi-head Latent Attention (MLA)[DALF+24]. Equipped with low-rank key-value joint compression, MLA achieves better performance than MHA, but requires a significantly smaller amount of KV cache.

Preliminaries: Standard Multi-Head Attention

Let \(d\) be the embedding dimension, \(n_h\) be the number of attention heads, \(d_h\) be the dimension per head, and \(\mathbf{h}_{t}\in\mathbb{R}^{d}\) be the attention input of the \(t\)-th token. Standard MHA first produces \(\mathbf{q}_{t},\mathbf{k}_{t}, \mathbf{v}_{t}\in\mathbb{R}^{d_{h}n_h}\) through three matrices \(W^Q,W^K,W^V\in\mathbb{R}^{d_{h}n_{h}\times{d}}\), respectively:

\[\mathbf{q}_{t} = W^{Q}\mathbf{h}_{t}\]

\[\mathbf{k}_{t} = W^{K}\mathbf{h}_{t}\]

\[\mathbf{v}_{t} = W^{V}\mathbf{h}_{t}\]

Then, \(\mathbf{q}_{t}, \mathbf{k}_{t}, \mathbf{v}_{t}\) will be sliced into \(n_h\) heads for the multi-head attention computation:

\[[\mathbf{q}_{t,1};\mathbf{q}_{t,2};\dots;\mathbf{q}_{t,n_h}] = \mathbf{q}_{t}\]

\[[\mathbf{k}_{t,1};\mathbf{k}_{t,2};\dots;\mathbf{k}_{t,n_h}] = \mathbf{k}_{t}\]

\[[\mathbf{v}_{t,1};\mathbf{v}_{t,2};\dots;\mathbf{v}_{t,n_h}] = \mathbf{v}_{t}\]

\[\mathbf{o}_{t,i} = \sum_{j=1}^{t}\text{Softmax}_{j}\left(\frac{\mathbf{q}_{t,i}^{\intercal}\mathbf{k}_{j,i}}{\sqrt{d_h}}\right)\mathbf{v}_{j,i}\]

\[\mathbf{u}_{t} = W^{O}[\mathbf{o}_{t,1};\mathbf{o}_{t,2};\dots;\mathbf{o}_{t,n_h}]\]

where \(\mathbf{q}_{t,i},\mathbf{k}_{t,i},\mathbf{v}_{t,i}\in\mathbb{R}^{d_h}\) denote the query, key, and value of the \(i\)-th attention head; \(W^{O}\in\mathbb{R}^{d\times{d_{h}n_{h}}}\) denotes the output projection matrix.

Fig. 2 Multi-Head Attention, the red text indicates that it needs to be cached.

Tip

During inference, all keys and values need to be cached to accelerate inference (the keys and values need to be computed only once), so MHA needs to cache \(2n_{h}d_{h}l\) (\(l\) denote layer num) elements for each token. In model deployment, this heavy KV cache is a large bottleneck that limits the maximum batch size and sequence length.

Low-Rank Key-Value Joint Compression

The core of MLA is the low-rank joint compression for keys and values to reduce KV cache:

\[\mathbf{c}_{t}^{KV} = W^{DKV}\mathbf{h}_{t}\]

\[\mathbf{k}_{t}^{C} = W^{UK}\mathbf{c}_{t}^{KV}\]

\[\mathbf{v}_{t}^{C} = W^{UV}\mathbf{c}_{t}^{KV}\]

where \(\mathbf{c}_{t}^{KV}\in\mathbb{R}^{d_c}\) is the compressed latent vector for keys and values, \(d_c\ll d_{h}n_{h}\) denotes the KV compression dimension, \(W^{DKV}\in\mathbb{R}^{d_{c}\times d}\) and \(W^{UK},W^{UV}\in\mathbb{R}^{d_{h}n_{h}\times d_c}\). During inference, MLA only needs to cache \(\mathbf{c}_{t}^{KV}\), so its KV cache has only \(d_{c}l\) elements.

Fig. 3 Core of MLA: low-rank key-value joint compression.

In addition, during inference (omit index \(i\) for brevity):

\[\begin{split} \begin{aligned} \mathbf{q}_{t}^{\intercal}\mathbf{k}_{j}^{C} &= (W^{Q}\mathbf{h}_{t})^{\intercal}W^{UK}\mathbf{c}_{j}^{KV}\\ &= \mathbf{h}_{t}^{\intercal}(W^{Q})^{\intercal}W^{UK}\mathbf{c}_{j}^{KV}\\ &= \mathbf{h}_{t}^{\intercal}((W^{UK})^{\intercal}W^{Q})^{\intercal}\mathbf{c}_{j}^{KV}\\ &= ((W^{UK})^{\intercal}W^{Q}\mathbf{h}_{t})^{\intercal}\mathbf{c}_{j}^{KV} \end{aligned} \end{split}\]

\(W^{UK}\) can be absorbed into \(W^{Q}\), that is:

\[W^{Q}\leftarrow(W^{UK})^{\intercal}W^{Q}.\]

Similarily, \(W^{UV}\) can be absorbed into \(W^{O}\). We even do not need to compute keys and values out for attention.

Tip

In order to reduce the activation memory during training (count params), we also perform low-rank compression for the queries, even if it cannot reduce the KV cache:

\[\mathbf{c}_{t}^{Q} = W^{DQ}\mathbf{h}_{t}\]

\[\mathbf{q}_{t}^{C} = W^{UQ}\mathbf{c}_{t}^{Q}\]

where \(\mathbf{c}_{t}^{Q}\in\mathbb{R}^{{d_{c}}'}\) is the compressed latent vector for queries, \({d_c}'\ll d_{h}n_{h}\) denotes the query compression dimension, \(W^{DQ}\in\mathbb{R}^{{d_c}'\times d}\) and \(W^{UQ}\in\mathbb{R}^{d_{h}n_{h}\times {d_c}'}\).

Fig. 4 Compression for queries.

Decoupled Rotary Position Embedding

RoPE[SLP+23] is position-sensitive for both keys and queries:

\[\begin{split} \begin{aligned} \text{RoPE}(\mathbf{q}_{t,i})^{\intercal}\text{RoPE}(\mathbf{k}_{j,i}^{C}) &= \text{RoPE}(W^{Q,i}\mathbf{h}_{t})^{\intercal}\text{RoPE}(W^{UK,i}\mathbf{c}_{j}^{KV}) \\ &= (\mathcal{R}_{t}W^{Q,i}\mathbf{h}_{t})^{\intercal}\mathcal{R}_{j}W^{UK,i}\mathbf{c}_{j}^{KV}\\ &= \mathbf{h}_{t}^{\intercal}(\mathcal{R}_{t}W^{Q,i})^{\intercal}\mathcal{R}_{j}W^{UK,i}\mathbf{c}_{j}^{KV}\\ &= \mathbf{h}_{t}^{\intercal}(W^{Q,i})^{\intercal}(\mathcal{R}_{t})^{\intercal}\mathcal{R}_{j}W^{UK,i}\mathbf{c}_{j}^{KV} \end{aligned} \end{split}\]

\(W^{UK}\) cannot be absorbed into \(W^{Q}\) any more during inference, since a RoPE matrix related to the currently generating token will lie between \(W^{Q}\) and \(W^{UK}\) and matrix multiplication does not obey a commutative law.

As a solution, we propose the decoupled RoPE strategy that uses additional multi-head queries \(\mathbf{q}_{t,i}^{R}\in\mathbb{R}^{d_h^{R}}\) and a shared key \(\mathbf{k}_{t}^{R}\in\mathbb{R}^{d_h^{R}}\) to carry RoPE, where \(d_{h}^{R}\) denotes the per-head dimension of the decoupled queries and key. Equipped with the decoupled RoPE strategy, MLA performs the following computation:

\[\begin{split} \begin{aligned} \left[\mathbf{q}_{t,1}^{R},\mathbf{q}_{t,2}^{R},\dots,\mathbf{q}_{t,n_h}^{R}\right] = \mathbf{q}_{t}^{R} &= \text{RoPE}(W^{QR}\mathbf{c}_{t}^{Q})\\ \mathbf{k}_{t}^{R} &= \text{RoPE}(W^{KR}\mathbf{h}_t)\\ \mathbf{q}_{t,i} &= [\mathbf{q}_{t,i}^{C};\mathbf{q}_{t,i}^{R}]\\ \mathbf{k}_{t,i} &= [\mathbf{k}_{t,i}^{C};\mathbf{k}_{t}^{R}]\\ \mathbf{o}_{t,i} &= \sum_{j=1}^{t}\text{Softmax}_{j}\left(\frac{\mathbf{q}_{t,i}^{\intercal}\mathbf{k}_{j,i}}{\sqrt{d_h+d_{h}^{R}}}\right)\mathbf{v}_{j,i}\\ \mathbf{u}_{t} &= W^{O}[\mathbf{o}_{t,1};\mathbf{o}_{t,2};\dots;\mathbf{o}_{t,n_h}] \end{aligned} \end{split}\]

where \(W^{QR}\in\mathbb{R}^{d_{h}^{R}n_{h}\times {d_{c}}'}\) and \(W^{KR}\in\mathbb{R}^{d_{h}^{R}n_{h}\times d}\) are matrices to produce the decouples queries and key. During inference, the decoupled key should also be cached. Therefore, DeepSeek-V2 requires a total KV cache containing \((d_c+d_{h}^{R})l\) elements.

Fig. 5 Multi-head Latent Attention.

Tip

MLA uses decoupled keys and queries to carry RoPE, where keys are shared across tokens to save cache.