Scaling Relationship on Learning Mathematical Reasoning with Large Language Models

Scaling Relationship on Learning Mathematical Reasoning with Large Language Models#

Note

The target of this paper is to try to understand the performances of supervised LLMs in math reasoning. We expect a pre-trained LLM \(\rho\) to learn reasoning ability from a supervised reasoning dataset \(\mathcal{D}\). The dataset is defined by \(\mathcal{D} = \{q_i, r_i, a_i\}_i\), where \(q\) is a question, \(r\) is a chain-of-thought reasoning path, and \(a\) is a numerical answer. We perform supervised fine-tuning on dataset \(\mathcal{D}\) to obtain an SFT model \(\pi\). We use \(\pi\) to generate reasoning paths and answers in the test set by greedy decoding and report the accuracy as our metric here.

Model Accuracy VS. Pre-training Loss#

We analyze the SFT and ICL (8-shot) performance of GPT-3, LLaMA, LLaMA2, and GPT-4. The pre-training losses of these models are observed in their paper. We use the results of GPT-3 fine-tuning from[CKB+21] and we fine-tune LLaMA and LLaMA2 on the GSM8K training set.

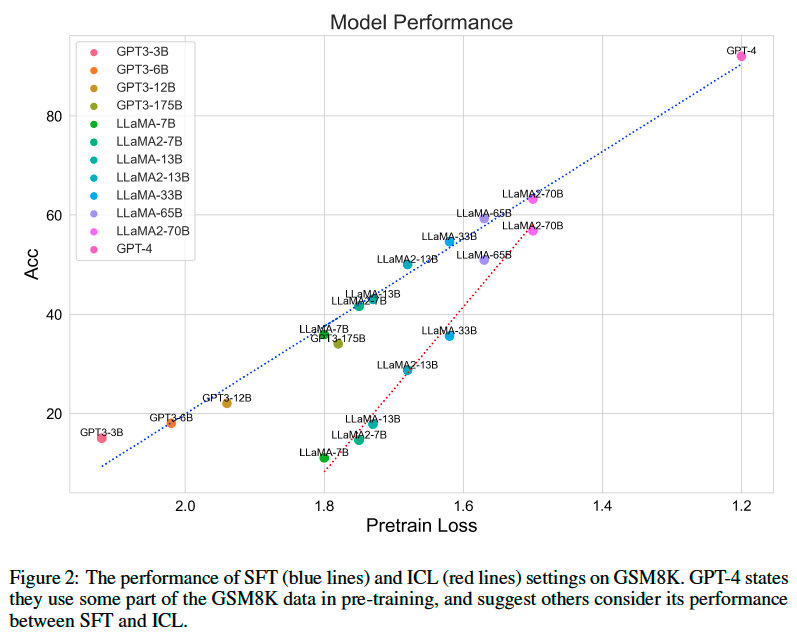
../_images/rs-1.png

We can find that:

  • The pre-training losses are approximately negatively linear correlated to the SFT and ICL accuracy during the given pre-training loss interval.

  • SFT outperforms ICL consistently, while the improvements diminish when the pre-training loss is lower.

From the observations, one effective way to improve reasoning ability is to train a better base model with lower pre-training loss (Pre-training is all you need!).

Model Accuracy VS. Supervised Data Count#

Supervised fine-tuning does improve LLMs’ reasoning ability, we want to know how the supervised data amount influences the model’s improvement. We fine-tune LLaMA and LLaMA2 with {1, 1/2, 1/4, 1/8, 1/16, 1/32} amount of the training set from GSM8K.

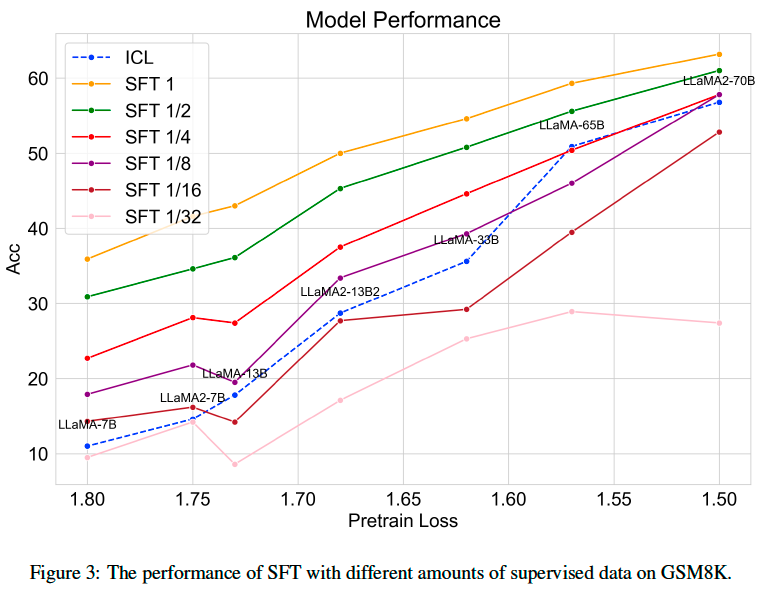
../_images/rs-2.png

From the figure, we can observe that:

  • The model performance has a log-linear relation versus data amount.

  • Better model needs more amount of data to outperform its ICL performance.

  • Better model benefits less when supervised data amount doubles.

From the observation, it is straightforward to enlarge the training dataset to improve the performance, especially for worse models. For better models, it benefits less which echoes that better models have learned more reasoning ability during pre-training.

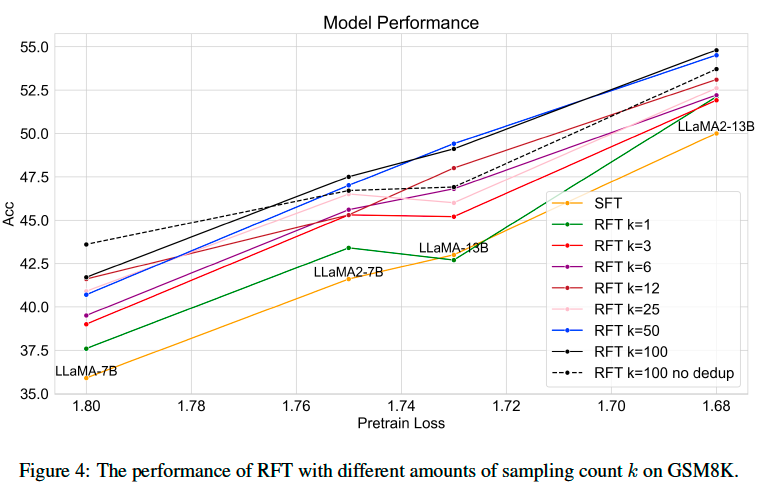
Model Accuracy VS. Augmented Data Count#

Increasing the amount of math reasoning labeled data is difficult, especially proposing a new question. We find a simplified version of rejection sampling is a naive and effective way to augment new reasoning paths and can improve the model performance. And we find the key factor influences fine-tuning on rejection sampling (RFT) augmented data is distinct reasoning path amount.

Rejection Sampling Fine-tuning The SFT model \(\pi\) obtains the ability to perform zero-shot chainof- thought reasoning, and we use \(\pi\) to generate more correct reasoning paths \(r_{ij}\) to supply the training dataset. For each \(q_i\), we generate \(k\) candidate reasoning paths and answers \(r\), \(a\) with a temperature of 0.7. We first filter out reasoning paths with wrong answers \(a\ne a_i\) or wrong calculations based on Python evaluation. Each reasoning path contains a list of equations \(e_j\) , and we select one reasoning path \(r_{ij}\) for each distinct equation list as the augmented data and remove other reasoning paths with the same list of equations to deduplicate similar reasoning paths. We define \(\mathcal{D}_{\pi}' = \mathcal{D}\cup\{q_i,r_{ij},a_i\}_{ij}\) as the augmented dataset. We fine-tune \(\mathcal{D}'\) on pre-trained LLM \(\rho\) to \(\pi_{\text{RFT}}\) as RFT.

../_images/rs-3.png
Contents