Understanding R1-Zero-Like Training

Understanding R1-Zero-Like Training#

Note

DeepSeek-R1-Zero has shown that reinforcement learning (RL) at scale can directly enhance the reasoning capabilities of LLMs without supervised fine-tuning.
In this work, we critically examine R1-Zero-like training by analyzing its two core components: base models and RL.

Analysis on Base Models#

We first investigate whether widely used open-source base models, which are typically trained for sentence completion (i.e. \(p_{\theta}(\mathbf{x})\)), can have their question-answering capabilities effectively elicited through appropriate templates.

../_images/r1-critic1.png

Experimental settings. For each base model, we apply each template to get the model responses, then let GPT-4o-mini to judge whether the model responses are in an answering format (regardless of quality). We record the percentage of responses that tend to answer the question as the metric. Finally, we evaluate the pass@8 accuracy of each model with the corresponding template to assess whether the base policies can explore rewarding trajectories for RL improvement.

Results. We suggests that DeepSeek-V3-Base is a nearly pure base model, while Qwen2.5 models are already SFT-like without templates. And aha moment already appears in base models including DeepSeek-V3-Base.

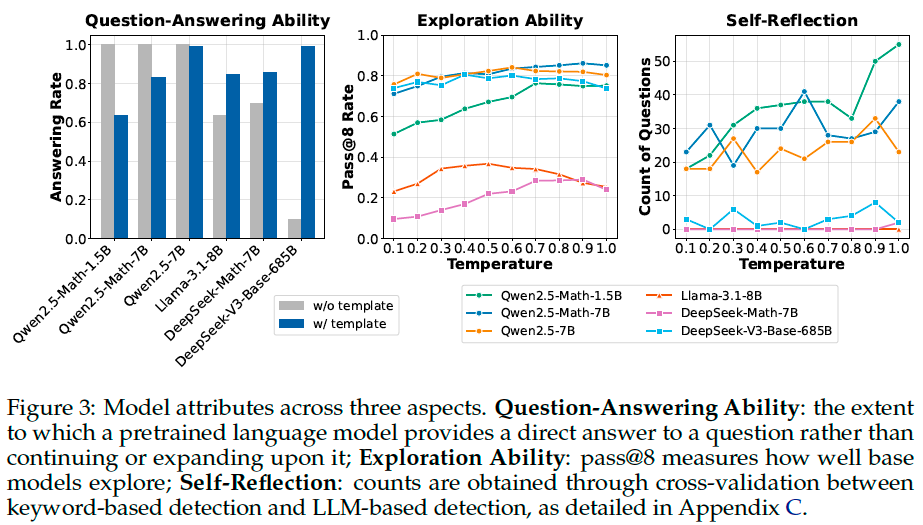
../_images/r1-critic2.png

Analysis on Reinforcement Learning#

GRPO objective function:

\[\begin{split} \begin{aligned} J_{GRPO}(\theta) = &\underset{q\sim P(Q),o\sim\pi_{\theta_{\text{old}}}(O|q)}{\mathbb{E}}\frac{1}{G}\sum_{i=1}^{G}\textcolor{red}{\frac{1}{|o_{i}|}}\sum_{t=1}^{|o_{i}|}\{\min\\ &\left[\frac{\pi_{\theta}(o_{i,t}|q,o_{i}<t)}{\pi_{\theta_{\text{old}}}(o_{i,t}|q,o_{i}<t)}\hat{A}_{i,t}, \text{clip}\left(\frac{\pi_{\theta}(o_{i,t}|q,o_{i}<t)}{\pi_{\theta_{\text{old}}}(o_{i,t}|q,o_{i}<t)}, 1-\epsilon, 1+\epsilon\right)\hat{A}_{i,t}\right], \end{aligned} \end{split}\]

where

\[ \hat{A}_{i, t} = \frac{R(q,o_i) - \text{mean}(R(q,o_1),\dots, R(q,o_G))}{\color{red}\text{std}(\{R(q,o_1),\dots, R(q,o_G)\})} \]

Compare to the objective function in PPO, GRPO introduces two biases:

  • Response-level length bias: This arises from dividing by \(|o_i|\). For positive advantages (\(\hat{A}_{i,t} > 0\), indicating a correct response), this bias results in greater gradient updates for shorter responses, leading the policy to favor brevity in correct answers. Conversely, for negative advantages, longer responses are penalized less due to their larger \(|o_i|\), causing the policy to prefer lengthier responses among incorrect ones.

  • Question-level difficulty bias: This is caused by dividing the centered outcome reward by \({\color{red}\text{std}(\{R(q,o_1),\dots, R(q,o_G)\})}\). Questions with lower standard deviations (e.g., those that are too easy or too hard) are given higher weights during policy updates.

Tip

Length Bias Also Exists in Open-Source PPO Implementations.

To avoid the aforementioned optimization bias in GRPO, we propose to simply remove the \(\color{red}\frac{1}{|o_i|}\) and \({\color{red}\text{std}(\{R(q,o_1),\dots, R(q,o_G)\})}\) normalization terms. We refer to our new optimization algorithm as Dr. GRPO.

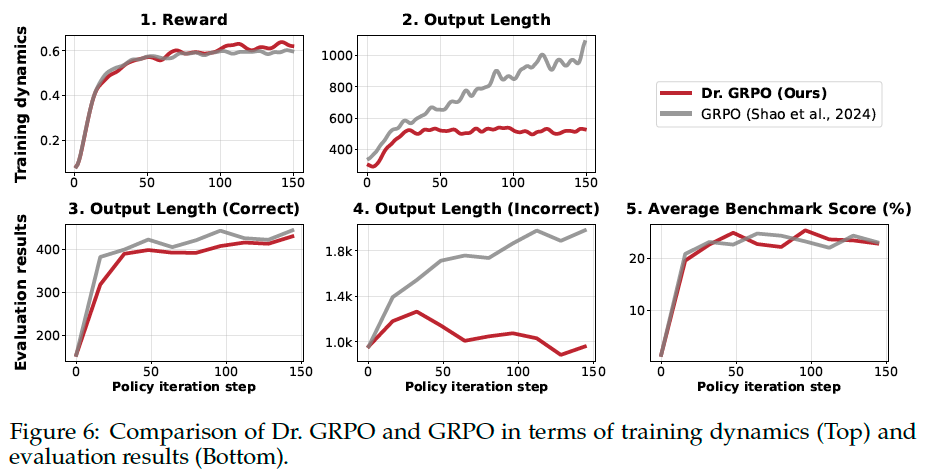
../_images/r1-critic3.png

Results. The length of incorrect responses is substantially reduced by Dr. GRPO compared to the baseline (Plot 4), suggesting that an unbiased optimizer also mitigates overthinking.

Contents