HumanEval

HumanEval#

Note

We evaluate functional correctness on a set of 164 handwritten programming problems, which we call the HumanEval[CTJ+21] dataset. Each problem includes a function signature, docstring, body, and several unit tests, with an average of 7.7 tests per problem.
Programming tasks in the HumanEval dataset assess language comprehension, reasoning, algorithms, and simple mathematics.

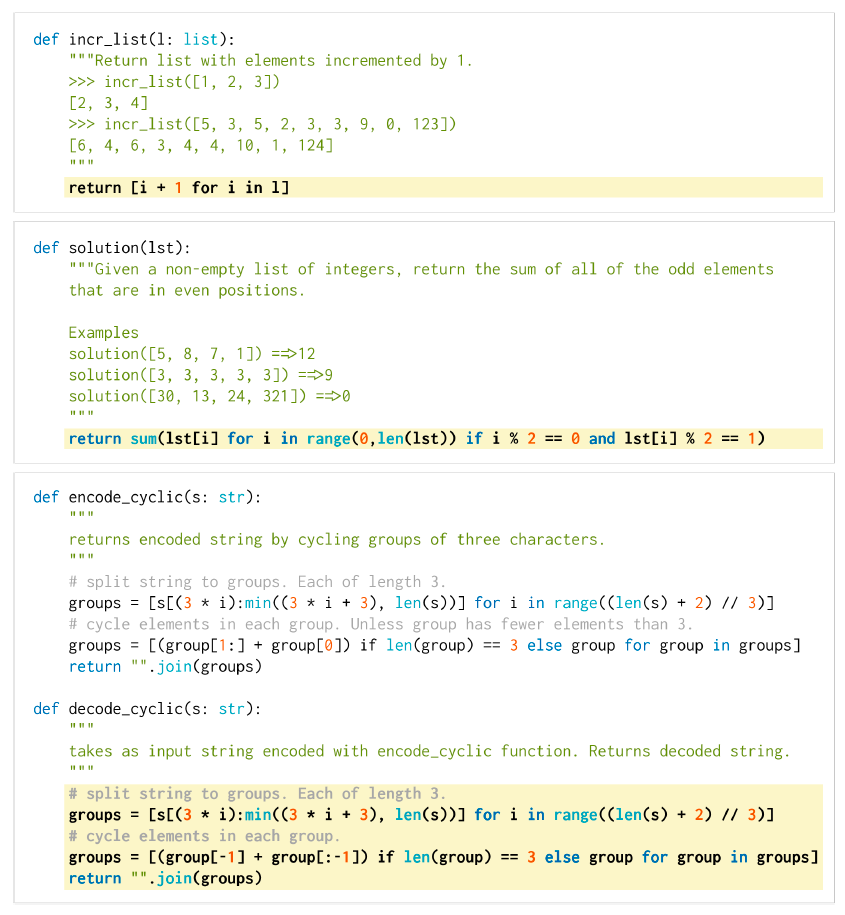
../_images/humaneval-3.png

Three example problems from the HumanEval dataset, where the probabilities that a single sample from Codex-12B passes unit tests are 0.9, 0.17, and 0.005. The prompt provided to the model is shown with a white background, and a successful model-generated completion is shown in a yellow background. Though not a guarantee for problem novelty, all problems were hand-written and not programmatically copied from existing sources.

Functional Correctness#

We evaluate functional correctness using the pass@\(k\) metric, where \(k\) code samples are generated per problem, a problem is considered solved if any sample passes the unit tests, and the total fraction of problems solved is reported. However, computing pass@\(k\) in this way can have high variance. Instead, to evaluate pass@\(k\), we generate \(n\ge k\) samples per task (in this paper, we use \(n = 200\) and \(k\le 100\)), count the number of correct samples \(c\le n\) which pass unit tests, and calculate the unbiased estimator

\[ \text{pass@}k := \mathbb{E}\left[1 - \frac{\binom{n-c}{k}}{\binom{n}{k}}\right] \]

Calculating this estimator directly results in very large numbers and numerical instability. We include a numerically stable numpy implementation that simplifies the expression and evaluates the product term-by-term.

import numpy as np

def pass_at_k(n, c, k):
    """
    :param n: total number of samples
    :param c: number of correct samples
    :param k: k in pass@$k$
    """
    if n - c < k: return 1.0
    return 1.0 - np.prod(1.0 - k / np.arange(n - c + 1, n + 1))
Contents