Flash Attention

Note

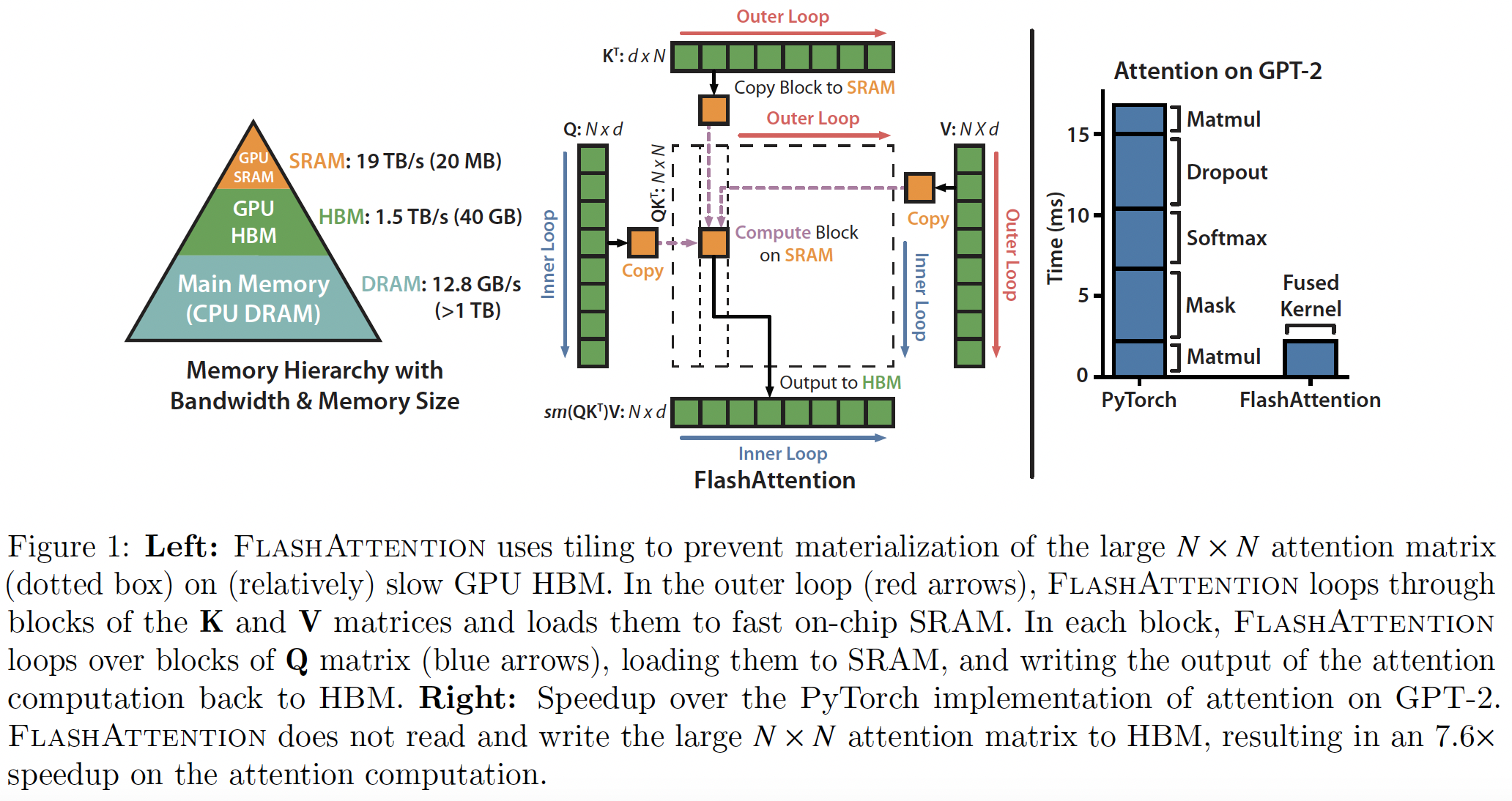
We propose FlashAttention, an IO-aware exact attention algorithm that uses tiling to reduce the number of memory reads/writes between GPU high bandwidth memory (HBM) and GPU on-chip SRAM.

Standard Attention Implementation

Given input sequences \(\mathbf{Q},\mathbf{K},\mathbf{V}\in\mathbb{R}^{N\times d}\) where \(N\) is the sequence length and \(d\) is the head dimension, we want to compute the attention output \(\mathbf{O}\in\mathbb{R}^{N\times d}\):

\[ \mathbf{S}=\mathbf{Q}\mathbf{K}^{\intercal}\in\mathbb{R}^{N\times N},\quad\mathbf{P}=\text{softmax}(\mathbf{S})\in\mathbb{R}^{N\times N},\quad \mathbf{O}=\mathbf{P}\mathbf{V}\in\mathbb{R}^{N\times d} \]

where softmax is applied row-wise.

An Efficient Attention Algorithm With Tiling and Recomputation

We apply two established techniques (tiling, recomputation) to overcome the technical challenge of computing exact attention in sub-quadratic HBM accesses. The main idea is that we split the inputs \(\mathbf{Q},\mathbf{K},\mathbf{V}\) into blocks, load them from slow HBM to fast SRAM, then compute the attention output with respect to those blocks. By scaling the output of each block by the right normalization factor before adding them up, we get the correct result at the end.

Tiling

We compute attention by blocks. Softmax couples columns of \(\mathbf{K}\), so we decompose the large softmax with scaling. For numerical stability, the softmax of vector \(x\in\mathbb{R}^{B}\) is computed as:

\[\begin{split} \begin{split} m(x) &:= \underset{i}{\max}x_i\\ f(x) &:= \left[e^{x_1-m(x)},\dots,e^{x_B-m(x)}\right]\\ l(x) &:= \sum_{i}f(x)_{i}\\ \text{softmax}(x) &:= \frac{f(x)}{l(x)} \end{split} \end{split}\]

For vectors \(x^{(1)},x^{(2)}\in\mathbb{R}^{B}\), we can decompose the softmax of the concatenated \(x=\left[x^{(1)},x^{(2)}\right]\in\mathbb{R}^{2B}\) as:

\[\begin{split} \begin{split} m(x) &:= m(\left[x^{(1)},x^{(2)}\right]) = \max(m(x^{(1)}), m(x^{(2)}))\\ f(x) &:= \left[e^{m(x^{(1)})-m(x)}f(x^{(1)}),e^{m(x^{(2)})-m(x)}f(x^{(2)})\right]\\ l(x) &:= l(\left[x^{(1)},x^{(2)}\right]) = e^{m(x^{(1)})-m(x)}l(x^{(1)}) + e^{m(x^{(2)})-m(x)}l(x^{(2)})\\ \text{softmax}(x) &:= \frac{f(x)}{l(x)} \end{split} \end{split}\]

Therefore if we keep track of some extra statistics (\(m(x),l(x)\)), we can compute softmax one block at a time.2 We thus split the inputs \(\mathbf{Q},\mathbf{K},\mathbf{V}\) into blocks.

Recomputation

One of our goals is to not store \(O(N^{2})\) intermediate values for the backward pass. The backward pass typically requires the matrices \(\mathbf{S},\mathbf{P}\in\mathbb{R}^{N\times N}\) to compute the gradients with respect to \(\mathbf{Q},\mathbf{K},\mathbf{V}\). However, by storing the output \(\mathbf{O}\) and the softmax normalization statistics \((m,l)\), we can recompute the attention matrix S and P easily in the backward pass from blocks of \(\mathbf{Q},\mathbf{K},\mathbf{V}\) in SRAM.

Algorithm

Tiling enables us to implement our algorithm in one CUDA kernel, loading input from HBM, performing all the computation steps (matrix multiply, softmax, optionally masking and dropout, matrix multiply), then write the result back to HBM. This avoids repeatedly reading and writing of inputs and outputs from and to HBM.

where \(\text{diag}(v)\) means a square diagonal matrix with the elements of vector \(v\) on the main diagonal.