Training Language Models to Self-Correct via Reinforcement Learning

Note

Training self-correction via SFT either suffers from a distribution mismatch between the training data and the model’s own responses (Pair-SFT), or implicitly prefers only making minor edits (STaR).
SCoRe is a multi-turn reinforcement learning approach, that directly train on self-generated data, it has two stages:

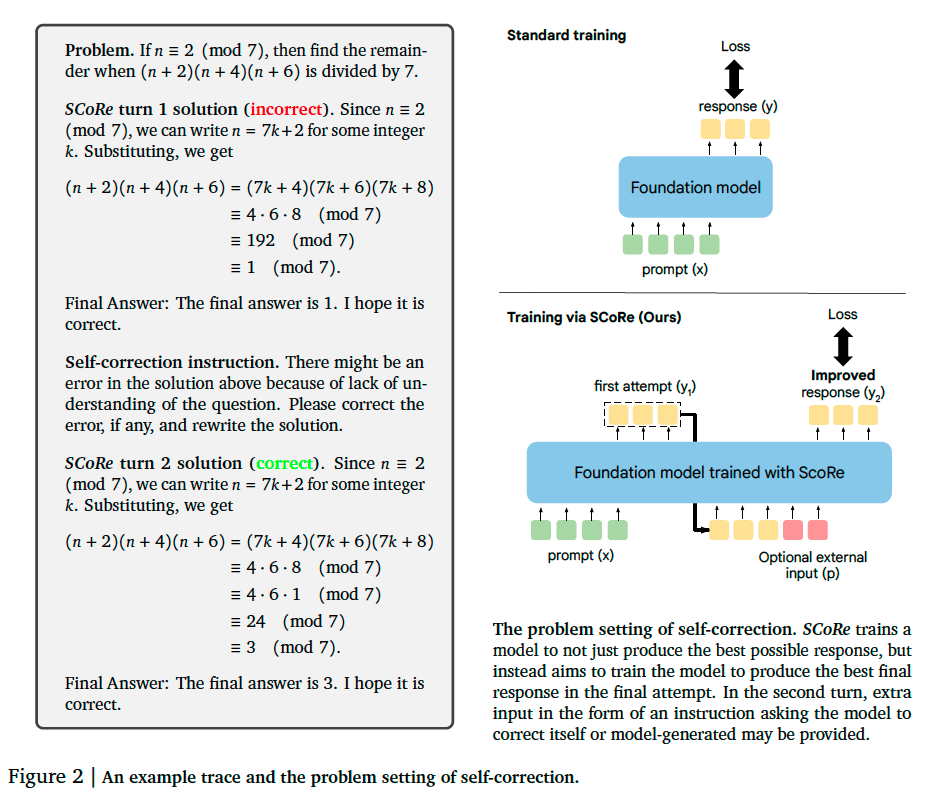
• stage 1: produce high-reward revisions at the second attempt, while forcing the model to not change its first-attempt response.

• stage 2: trains responses at both attempts towards optimizing reward, and reward shaping to incentivize self-correction.

Preliminaries and Problem Setup

Our goal is to develop an approach for training LLMs to improve their own predictions by entirely training on self-generated data.

Concretely, given a dataset \(\mathcal{D} = \{(x_{i}, y_{i}^{\ast})_{i=1}^{N}\}\) of problems \(x_{i}\) and oracle responses \(y_{i}^{\ast}\), we will train an LLM policy \(\pi_{\theta}(\cdot|[x,\hat{y}_{1:l},p_{1:l}])\) that, given the problem \(x\), previous \(l\) model attempts \(\hat{y}_{1:l}\) at the problem, and auxiliary instructions \(p_{1:l}\) (e.g., instruction to find a mistake and improve the response), solves the problem \(x\) as correctly as possible.

Moreover, we assume access to a reward function / verifier \(\hat{r}(y, y^{\ast})\), such as a string-matching based answer checking function that evaluates correctness of response \(y\) by comparing with the oracle response \(y^{\ast}\). Critically, we do not assume access to such a function at test-time and the model itself learns to deduce whether there was a mistake and corrects it.

We aim to find a model \(\pi\) that maximizes the correctness reward obtained from the verifier at the end of \(l+1\) turns:

\[ \underset{\pi_{\theta}}{\max}\mathbb{E}_{x,y^{\ast}\sim\mathcal{D},\hat{y}_{l+1}\sim\pi_{\theta}(\cdot|[x,\hat{y}_{1:l},p_{1:l}])}\left[\hat{r}(\hat{y}_{l+1},y^{\ast})\right] \]

SCoRe: Self-Correction via Multi-Turn Reinforcement Learning

Stage I: Training a Model Initialization to Prevent Collapse

We explicitly fine-tune the base model to produce high-reward revisions at the second attempt, while forcing the model to not change its first-attempt response. This stage is critical in reducing the base model’s bias towards simply coupling the first and second-attempt distributions, and thus becoming trapped in a local optima when actual multi-turn RL is run.

\[ \underset{\pi_{\theta}}{\max}\mathbb{E}_{x_1,y_1\sim\pi_{\theta}(\cdot|x_1),y_{2}\sim\pi_{\theta}(\cdot|[x_1,p_1])}\left[\hat{r}(y_{2},y^{\ast}) - \beta_{2}\log(\pi_{\theta}(y_1|x_1)/\pi_{\text{ref}}(y_1|x_1))\right] \]

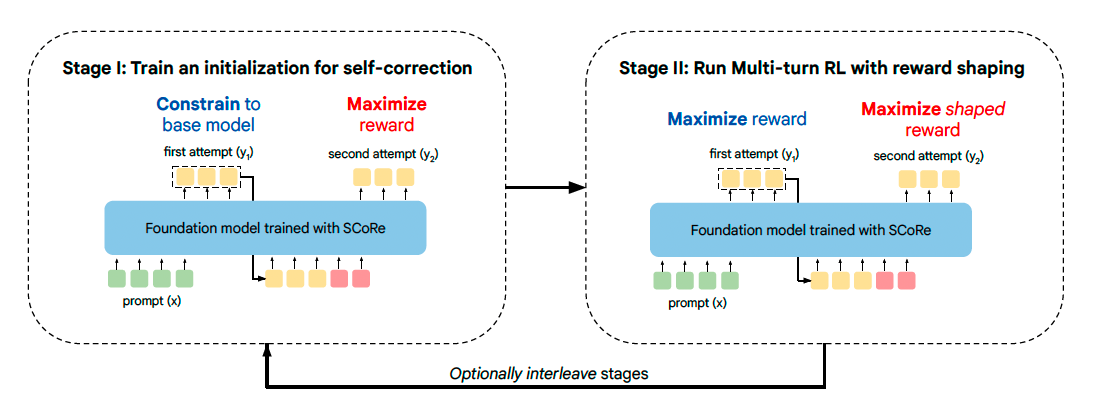
Stage II: Multi-Turn RL with Reward Shaping

Equipped with a model initialization from Stage I that exhibits a substantially smaller bias to couple the two responses, the second stage of SCoRe now trains responses at both attempts towards optimizing reward (\(x_2\) denotes all the tokens from the first turn concatenated with each other):

\[ \underset{\pi_{\theta}}{\max}\mathbb{E}_{x_1,y_1\sim\pi_{\theta}(\cdot|x_1),y_{2}\sim\pi_{\theta}(\cdot|[x_1,p_1])}\left[\sum_{i=1}^{2}\hat{r}(y_{i},y^{\ast}) - \beta_{1}\log(\pi_{\theta}(y_i|x_i)/\pi_{\text{ref}}(y_i|x_i))\right] \]

Reward shaping to incentivize self-correction. It is unclear if running RL for optimizing the above Equation prefers a strategy that incentivizes self-correction over finding the best first-attempt response and keeping it unchanged, to mitigate this issue, given an two-turn on-policy rollout \(\tau = \{x_1, \hat{y}_1, \hat{r}(y_1, y^{\ast}), x_2, \hat{y}_{2}, \hat{r}(y_2, y^{\ast})\}\), we propose to modify the reward \(\hat{r}(y_2, y^{\ast})\) with an additional bonus given by:

\[ \hat{b}(y_2|y_1,y^{\ast}) = \alpha\cdot(\hat{r}(y_2,y^{\ast}) - \hat{r}(y_1,y^{\ast})) \]

Adding this bonus to the second attempt only emphasizes traces that flip the correctness of the response and assigns a heavy negative penalty to transitions that change a correct response to incorrect in the second attempt.

Tip

SCoRe applies stages I and II in an interleaved fashion for multiple iterations.