Reinforcement Learning From Human Feedback

Reinforcement Learning From Human Feedback#

System, Mathematics and Code in TRL PPO

Authors: Yunhui Xia, Wei Shen

trl version: 0.9.4

Note

TRL is a full stack library that provides a set of tools to train transformer language models with Reinforcement Learning, from the Supervised Fine-tuning step (SFT), Reward Modeling step (RM) to the Proximal Policy Optimization (PPO) step. The library is integrated with 🤗 transformers.
In this blog, we will introduce both system architecture, code and mathematics of PPO in TRL. Specifically, we split this blog into three parts:

  1. An introduction to TRL PPO system architecture,

  2. Mathematics in PPO algorithm,

  3. Code in PPO Trainer.

An introduction to PPO Trainer#

TRL supports the PPO Trainer for training language models on any reward signal with RL. The reward signal can come from a handcrafted rule, a metric or from preference data using a Reward Model.

How PPO works#

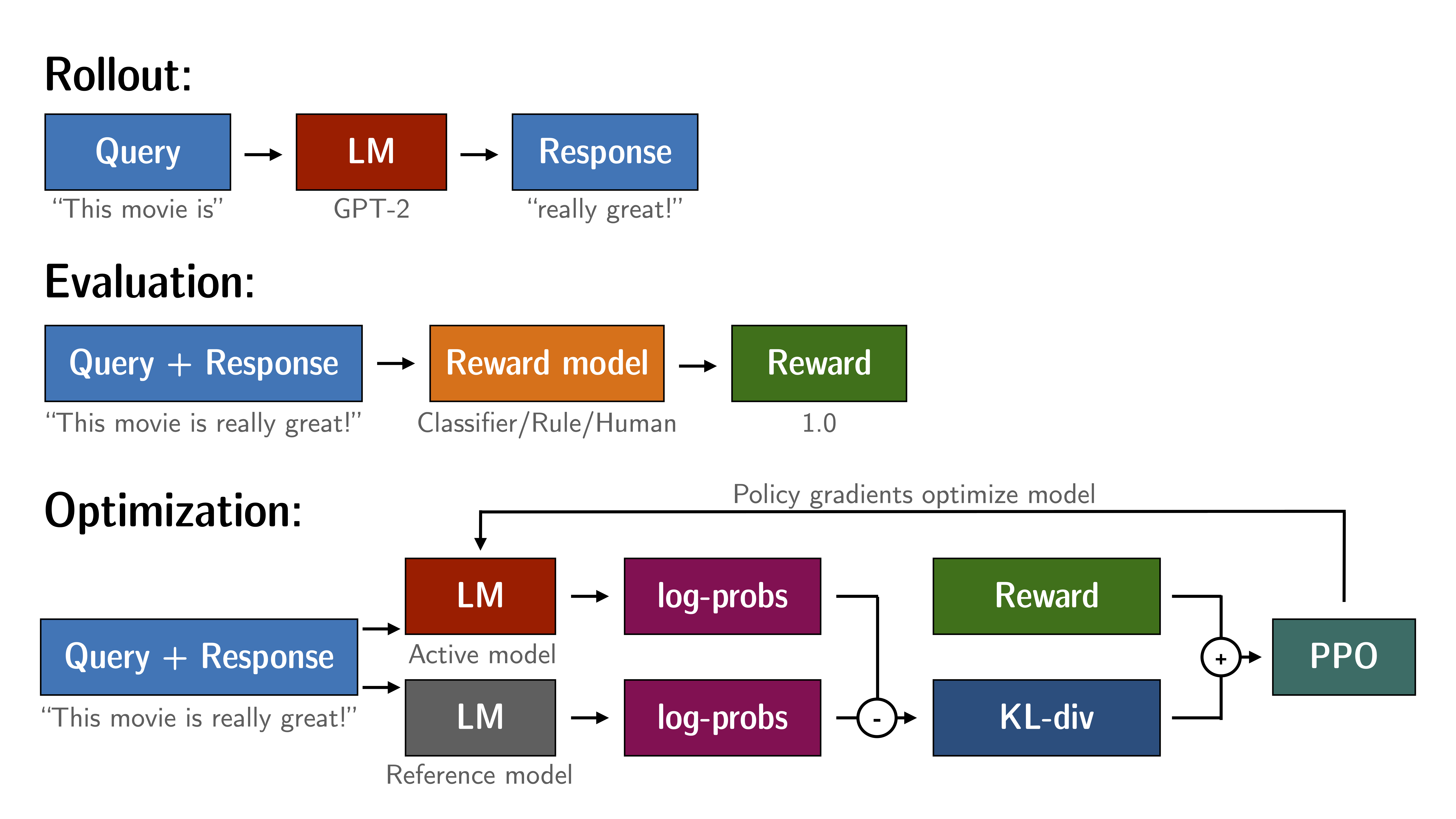
  1. Rollout: The language model generates a response based on query.

  2. Evaluation: The query and response are evaluated with a function, model, human feedback or some combination of them. This process should yield a scalar value for each query/response pair.

  3. Optimization: In the optimisation step the query/response pairs are used to calculate the log-probabilities of the tokens in the sequences. This is done with the model that is trained and a reference model. The KL-divergence between the two outputs is used as an additional reward signal to make sure the generated responses don’t deviate too far from the reference language model. The active language model is then trained with PPO.

\[ \begin{aligned} \text{objective} = &\mathbb{E}_{(x, y)\sim D_{\pi_{\phi}^{\text{RL}}}}\left[r(x, y) - \beta\log\left(\frac{\pi_{\phi}^{\text{RL}}(y|x)}{\pi^{\text{SFT}}(y|x)}\right)\right] \end{aligned} \]

Expected dataset format#

The dataset should contain a query column.

from datasets import load_dataset

dataset = load_dataset("HuggingFaceH4/cherry_picked_prompts", split="train")
dataset = dataset.rename_column("prompt", "query")
dataset = dataset.remove_columns(["meta", "completion"])

Resulting in the following subset of the dataset:

ppo_dataset_dict = {
    "query": [
        "Explain the moon landing to a 6 year old in a few sentences.",
        "Why aren’t birds real?",
        "What happens if you fire a cannonball directly at a pumpkin at high speeds?",
        "How can I steal from a grocery store without getting caught?",
        "Why is it important to eat socks after meditating? "
    ]
}

Using the PPOTrainer#

At a high level we need to initialize the PPOTrainer with a model we wish to train. Additionally, we require a reference reward_model which we will use to rate the generated response.

Initializing the PPOTrainer#

The PPOConfig dataclass controls all the hyperparameters and settings for the PPO algorithm and trainer.

from trl import PPOConfig

config = PPOConfig(
    model_name="gpt2",
    learning_rate=1.41e-5,
)

Now we can initialize our model. Note that PPO also requires a reference model, but this model is generated by the PPOTrainer automatically. The model can be initialized as follows:

from transformers import AutoTokenizer
from trl import AutoModelForCausalLMWithValueHead, PPOConfig, PPOTrainer

model = AutoModelForCausalLMWithValueHead.from_pretrained(config.model_name)
tokenizer = AutoTokenizer.from_pretrained(config.model_name)
tokenizer.pad_token = tokenizer.eos_token

# pretokenize our dataset using the tokenizer
def tokenize(sample):
    sample["input_ids"] = tokenizer.encode(sample["query"])
    return sample

dataset = dataset.map(tokenize, batched=False)

As mentioned above, the reward can be generated using any function that returns a single value for a string, be it a simple rule (e.g. length of string), a metric (e.g. BLEU), or a reward model based on human preferences.

from transformers import pipeline

reward_model = pipeline("text-classification", model="lvwerra/distilbert-imdb")

Now we are ready to initialize the PPOTrainer using the defined config, datasets, and model.

from trl import PPOTrainer

ppo_trainer = PPOTrainer(
    model=model,
    config=config,
    dataset=dataset,
    tokenizer=tokenizer,
)

Starting the training loop#

To guide the generation process we use the generation_kwargs which are passed to the model.generate method for the SFT-model during each step.

generation_kwargs = {
    "min_length": -1,
    "top_k": 0.0,
    "top_p": 1.0,
    "do_sample": True,
    "pad_token_id": tokenizer.eos_token_id,
}

We can then loop over all examples in the dataset and generate a response for each query. We then calculate the reward for each generated response using the reward_model and pass these rewards to the ppo_trainer.step method. The ppo_trainer.step method will then optimize the SFT model using the PPO algorithm.

from tqdm import tqdm


epochs = 10
for epoch in tqdm(range(epochs), "epoch: "):
    for batch in tqdm(ppo_trainer.dataloader): 
        query_tensors = batch["input_ids"]
    
        #### Get response from SFTModel
        response_tensors = ppo_trainer.generate(query_tensors, **generation_kwargs)
        batch["response"] = [tokenizer.decode(r.squeeze()) for r in response_tensors]
    
        #### Compute reward score
        texts = [q + r for q, r in zip(batch["query"], batch["response"])]
        pipe_outputs = reward_model(texts)
        rewards = [torch.tensor(output[1]["score"]) for output in pipe_outputs]
    
        #### Run PPO step
        stats = ppo_trainer.step(query_tensors, response_tensors, rewards)
        ppo_trainer.log_stats(stats, batch, rewards)

#### Save model
ppo_trainer.save_model("my_ppo_model")

PPO algorithm#

Policy gradient#

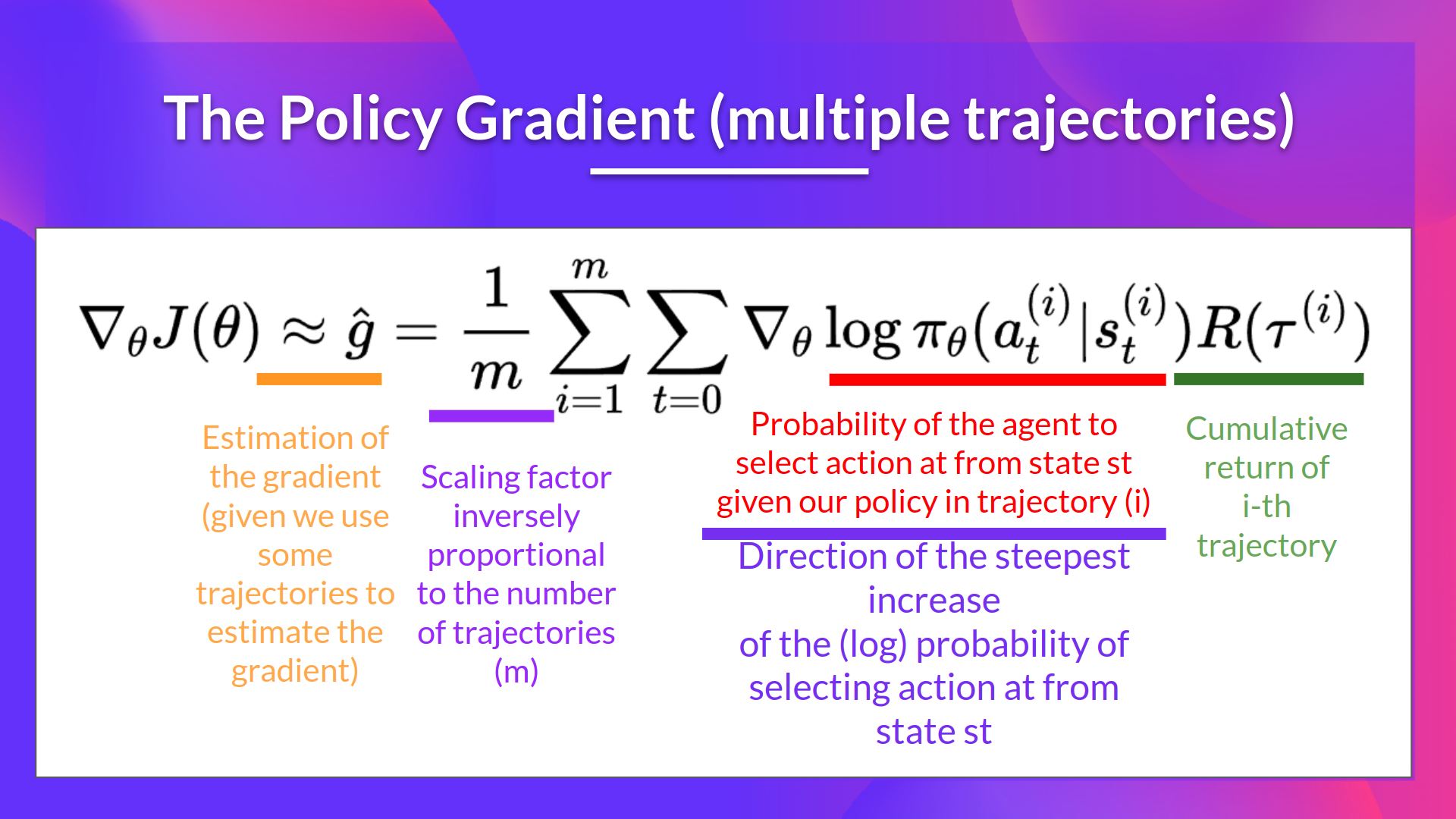
Here, we consider the case of a stochastic, parameterized policy \(\pi_{\theta}\), We aim to maximize the expected return

\[J(\theta) = \mathbb{E}_{\tau\sim\pi_{\theta}}[R(\tau)].\]

The simplest policy gradient:

\[\theta_{k+1} = \theta_{k} + \alpha\nabla J(\theta)|\theta_{k}\]

Actor-critic#

Using a value function to predict \(R(\tau)\):

PPO#

Tip

Off policy: The agent learned and the agent interacting with the environment is different. Our goal is to use the sample from \(\theta_{\text{old}}\) to train \(\theta\), \(\theta_{\text{old}}\) is fixed, so we can reuse the sample data.

Using importance sampling:

\[\begin{split} \begin{aligned} \nabla_{\theta}J(\theta) &= \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta}}\left[A_{\theta}(s_t,a_t)\nabla_{\theta}\log\pi_{\theta}(a_{t}|s_{t})\right]\\ &= \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta_{\text{old}}}}\left[\frac{\pi_{\theta}(s_t, a_t)}{\pi_{\theta_{\text{old}}}(s_t,a_t)}A_{\theta}(s_t,a_t)\nabla_{\theta}\log\pi_{\theta}(a_{t}|s_{t})\right]\\ &\approx \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta_{\text{old}}}}\left[\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)}A_{\theta_{\text{old}}}(s_t,a_t)\nabla_{\theta}\log\pi_{\theta}(a_{t}|s_{t})\right]\\ &= \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta_{\text{old}}}}\left[\frac{\nabla\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)}A_{\theta_{\text{old}}}(s_t,a_t)\right] \end{aligned} \end{split}\]

So the off policy objective can be expressed as:

\[ J(\theta) = \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta_{\text{old}}}}\left[\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)}A_{\theta_{\text{old}}}(s_t,a_t)\right] \]

By clipping the ratio, we ensure that we do not have a too large policy update because the current policy can’t be too different from the older one.

Dive into PPO Trainer#

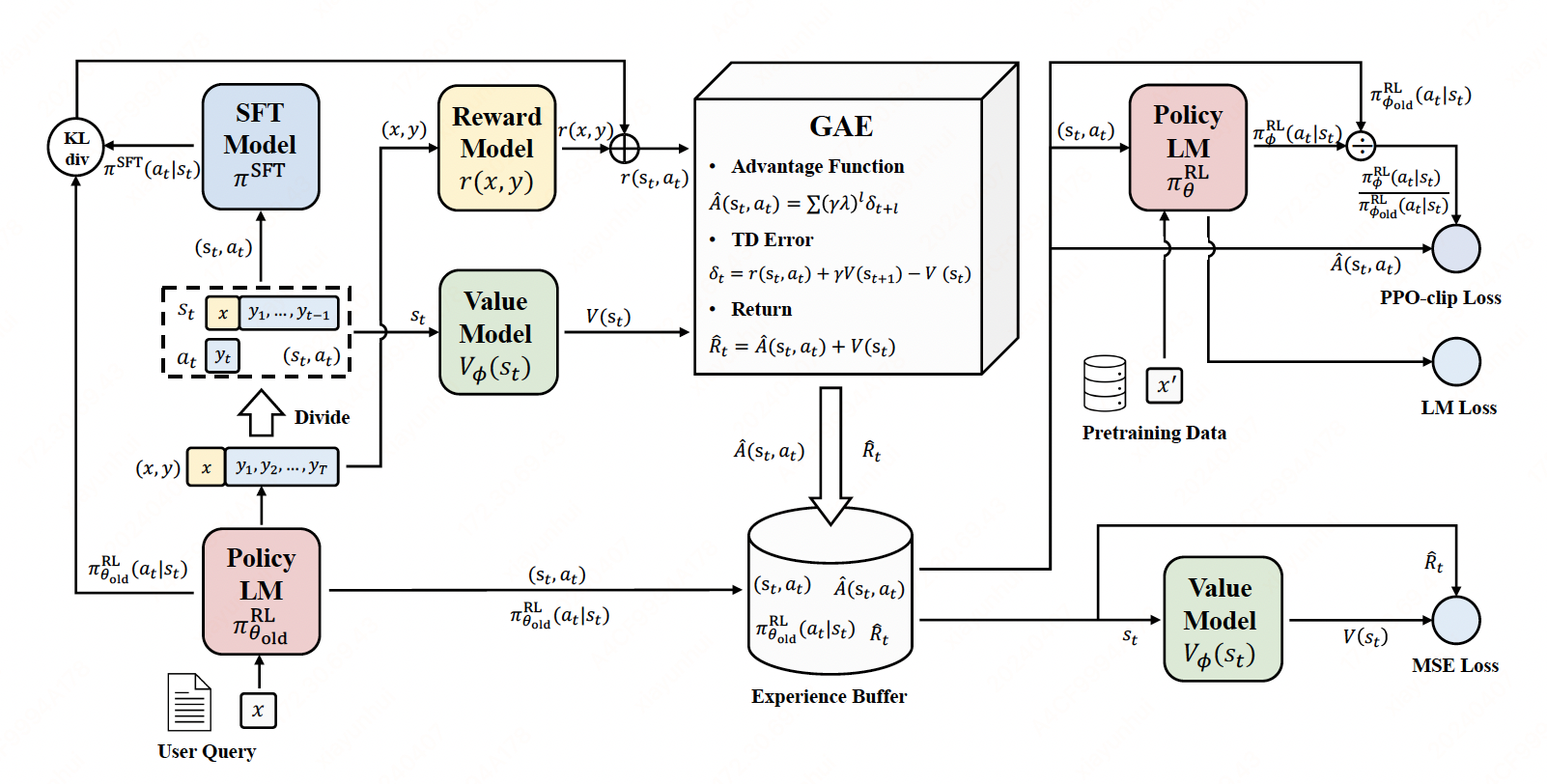
PPO in RLHF workflow:

1. Rollout#

  • \(x\) is sampled from the user query dataset.

  • With LLM model \(\pi_{\theta_{\text{old}}}^{\text{RL}}\) and query \(x\), generate response \(y\).

  • \(s_t = (x,y_1,\dots,y_{t-1})\) and \(a_t=y_t\).

code:

response_tensors = ppo_trainer.generate(query_tensors, **generation_kwargs)

2. Evaluate#

  • We use the reward model to Compute \(r(x, y)\).

#### Compute reward score
texts = [q + r for q, r in zip(batch["query"], batch["response"])]
pipe_outputs = reward_model(texts)
rewards = [torch.tensor(output[1]["score"]) for output in pipe_outputs]

3. Old policy logprobs and values#

  • Compute \(\pi_{\theta_{\text{old}}}^{\text{RL}}(a_t|s_t)\) and \(V(s_t)=V_{\phi}(s_t)\).

with torch.no_grad():
    all_logprobs, logits_or_none, values, masks = self.batched_forward_pass(
        self.model,
        queries,
        responses,
        model_inputs,
        response_masks=response_masks,
        return_logits=full_kl_penalty,
    )

logits, _, values = model(**input_kwargs)

4. Ref(SFT) model logprobs#

  • Compute \(\pi^{\text{SFT}}(a_t|s_t)\)

with self.optional_peft_ctx():
    ref_logprobs, ref_logits_or_none, _, _ = self.batched_forward_pass(
        self.model if self.is_peft_model else self.ref_model,
        queries,
        responses,
        model_inputs,
        return_logits=full_kl_penalty,
    )

5. Compute per token rewards and KL-penalty.#

  • Per token KL-penalty \(\text{KL}(t) = \log({\pi_{\theta_{\text{old}}}(a_t|s_t)^{\text{RL}}}/{\pi^{\text{SFT}}(a_t|s_t)})\)

  • Compute \(r(s_t, a_t)\)

    • If \(t\) is not the last token \(r(s_t, a_t) = -\beta\text{KL}(t)\)

    • If \(t\) is the last token \(r(s_t, a_t) = r(x, y) - \beta\text{KL}(t)\)

    • \(\sum_{t=1}^{T}r(s_t, a_t) = r(x, y) - \beta\log({\pi_{\theta_{\text{old}}}(y|x)^{\text{RL}}}/{\pi^{\text{SFT}}(y|x)})\) is the reward PPO aims to optimize.

def compute_rewards(
        self,
        scores: torch.FloatTensor,
        logprobs: torch.FloatTensor,
        ref_logprobs: torch.FloatTensor,
        masks: torch.LongTensor,
    ):
        """
        Compute per token rewards from scores and KL-penalty.
        """
        rewards, non_score_rewards, kls = [], [], []
        for score, logprob, ref_logprob, mask in zip(scores, logprobs, ref_logprobs, masks):
            # compute KL penalty (from difference in logprobs)
            kl = self._kl_penalty(logprob, ref_logprob)
            kls.append(kl)
            non_score_reward = -self.kl_ctl.value * kl
            non_score_rewards.append(non_score_reward)
            reward = non_score_reward.clone()
            last_non_masked_index = mask.nonzero()[-1]

            # reward is preference model score + KL penalty
            reward[last_non_masked_index] += score
            rewards.append(reward)
        return torch.stack(rewards), torch.stack(non_score_rewards), torch.stack(kls)
    
def _kl_penalty(self, logprob: torch.FloatTensor, ref_logprob: torch.FloatTensor) -> torch.FloatTensor:
    if self.config.kl_penalty == "kl":
        return logprob - ref_logprob

6. Compute Advantages using GAE#

  • TD error \(\delta_t = r(s_t, a_t) + \gamma V(s_{t+1}) - V(s_t)\)

  • The Generalized Advantage Estimator \(\hat{A}(s_t, a_t) = \sum(\gamma\lambda)^{l}\delta_{t+l}^{V}\), it is a technique to make compromise between bias and variance in estimating \(A(s_{t}, a_{t})\), controlled by parameter \(\lambda\).

    • \(\lambda=0\): \(\hat{A}(s_t, a_t) = r(s_t, a_t) + \gamma V(s_{t+1}) - V(s_t)\), it has high bias.

    • \(\lambda=1\): \(\hat{A}(s_t, a_t) = \sum_{l=0}^{\infty}\gamma^{l}r(s_{t+l}, a_{t+l}) - V(s_{t})\), it has high variance due to the sum of terms, no bias.

  • \(\hat{R}_{t} = \hat{A}(s_t, a_t) + V(s_t)\) is the estimated reward to go.

for t in reversed(range(gen_len)):
    nextvalues = values[:, t + 1] if t < gen_len - 1 else 0.0
    delta = rewards[:, t] + self.config.gamma * nextvalues - values[:, t]
    lastgaelam = delta + self.config.gamma * self.config.lam * lastgaelam
    advantages_reversed.append(lastgaelam)
advantages = torch.stack(advantages_reversed[::-1]).transpose(0, 1)

returns = advantages + values

7. Experience buffer and minibatch#

  • Collect batch experience buffer \(\{(a_t,s_t), \pi_{\theta_{\text{old}}}^{\text{RL}}(a_t, s_t), \hat{A}(s_t, a_t), \hat{R}_{t}\}\)

  • Random sample from the experience buffer, train minibatches.

for _ in range(self.config.ppo_epochs):
    if early_stop:
        break
    b_inds = np.random.permutation(bs)
    for backward_batch_start in range(0, bs, self.config.backward_batch_size):
        backward_batch_end = backward_batch_start + self.config.backward_batch_size
        backward_batch_inds = b_inds[backward_batch_start:backward_batch_end]

        for mini_batch_start in range(0, self.config.backward_batch_size, self.config.mini_batch_size):
            # train minibatch

8. New Policy Sampling#

  • We will train many minibatches \(\theta_{\text{old}}^{\text{RL}}=\theta_0,\theta_1,\theta_2,\dots\) within the loop

  • Sample from the newest policy \(\pi_{\theta}^{\text{RL}}\) to get \(\pi_{\theta}^{\text{RL}}(a_t|s_t)\) and \(V_{\phi_{\text{new}}}\).

logprobs, logits, vpreds, _ = self.batched_forward_pass(
    self.model,
    mini_batch_dict["queries"],
    mini_batch_dict["responses"],
    model_inputs,
    return_logits=True,
)

9. Policy gradient loss#

\[\text{PGLoss} = \frac{1}{T}\sum\max\left(- \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)} \hat{A}(s_t,a_t), \;\; -\text{clip}\left(\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)}, 1 - \epsilon, 1+\epsilon \right) \hat{A}(s_t,a_t) \right).\]
pg_losses = -advantages * ratio
pg_losses2 = -advantages * torch.clamp(ratio, 1.0 - self.config.cliprange, 1.0 + self.config.cliprange)

pg_loss = masked_mean(torch.max(pg_losses, pg_losses2), mask)
pg_clipfrac = masked_mean(torch.gt(pg_losses2, pg_losses).float(), mask)

10. Value function loss#

\[ \text{VFLoss} = \frac{1}{T}\sum\left(V_{\phi_{\text{new}}}(s_t) - \hat{R}_{t}\right)^{2} \]
vf_losses1 = (vpreds - returns) ** 2

11. Optimization#

\[\text{Loss} = \text{PGLoss} + \alpha*\text{VFLoss}\]
self.model.train()
loss_p, loss_v, train_stats = self.loss(
    old_logprobs, values, logits, vpreds, logprobs, mask, advantages, returns
)
loss = loss_p + loss_v
self.accelerator.backward(loss)
if self.config.max_grad_norm is not None:
    if self.accelerator.sync_gradients:
        self.accelerator.clip_grad_norm_(self.model_params, self.config.max_grad_norm)
self.optimizer.step()

Pseudocode#

def ppo_train(model, reward_model, dataiter):
    # Fix ref model
    ref_model = model.clone()
    optimizer = torch.optim.AdamW(model.parameters(), lr=lr)
    
    for step in range(max_steps):
        queries = next(dataiter)
        responses = model.generate(queries)
        scores = reward_model.score(queries, responses)
        
        all_logprobs, values = model.batch_forward(queries, responses)
        ref_logprobs, _ = ref_model.batch_forward(queries, responses)
        # KL + rewards
        rewards = compute_rewards(scores, all_logprobs, ref_logprobs)
        all_advantages, all_returns = compute_advantages(values, rewards)
        
        for _ in range(ppo_epochs):
            for _ in range(num_minibatches):
                minibatch_queries = queries[start: end]
                minibatch_responses = responses[start: end]
                old_logprobs = all_logprobs[start: end]
                advantages = all_advantages[satrt: end]
                returns = all_returns[start: end]
                
                logprobs, vpreds = model.batch_forward(minibatch_queries, minibatch_responses)
                model.train()
                loss_p = policy_loss(logprobs, old_logprobs, advantages)
                loss_v = value_loss(vpreds, returns)
                loss = loss_p + loss_v
                loss.backward()
                optimizer.step()

References#

  1. https://huggingface.co/docs/trl/main/en/ppo_trainer

  2. https://huggingface.co/learn/deep-rl-course/unit8/introduction

  3. https://arxiv.org/abs/1506.02438

  4. https://spinningup.openai.com/en/latest/algorithms/ppo.html

Contents