Two main approaches for solving RL problems

Note

Now that we learned the RL framework, how do we solve the RL problem? In other words, how do we build an RL agent that can select the actions that maximize its expected cumulative reward?

The Policy \(\pi\): the agent’s brain

The Policy \(\pi\) is the brain of our Agent, it’s the function that tells us what action to take given the state we are in. So it defines the agent’s behavior at a given time.

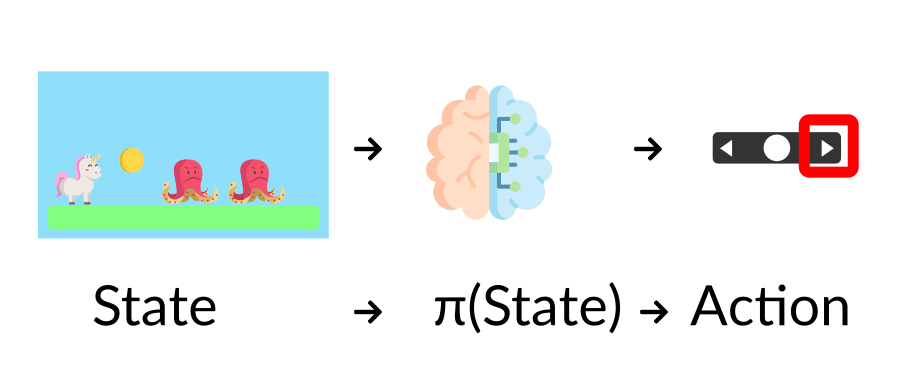
This Policy is the function we want to learn, our goal is to find the optimal policy \(\pi^{\ast}\), the policy that maximizes expected return when the agent acts according to it. There are two approaches to train our agent to find this optimal policy \(\pi^{\ast}\):

• Directly, by teaching the agent to learn which action to take, given the current state: Policy-Based Methods.

• Indirectly, teach the agent to learn which state is more valuable and then take the action that leads to the more valuable states: Value-Based Methods.

Policy-Based Methods

In Policy-Based methods, we learn a policy function directly.

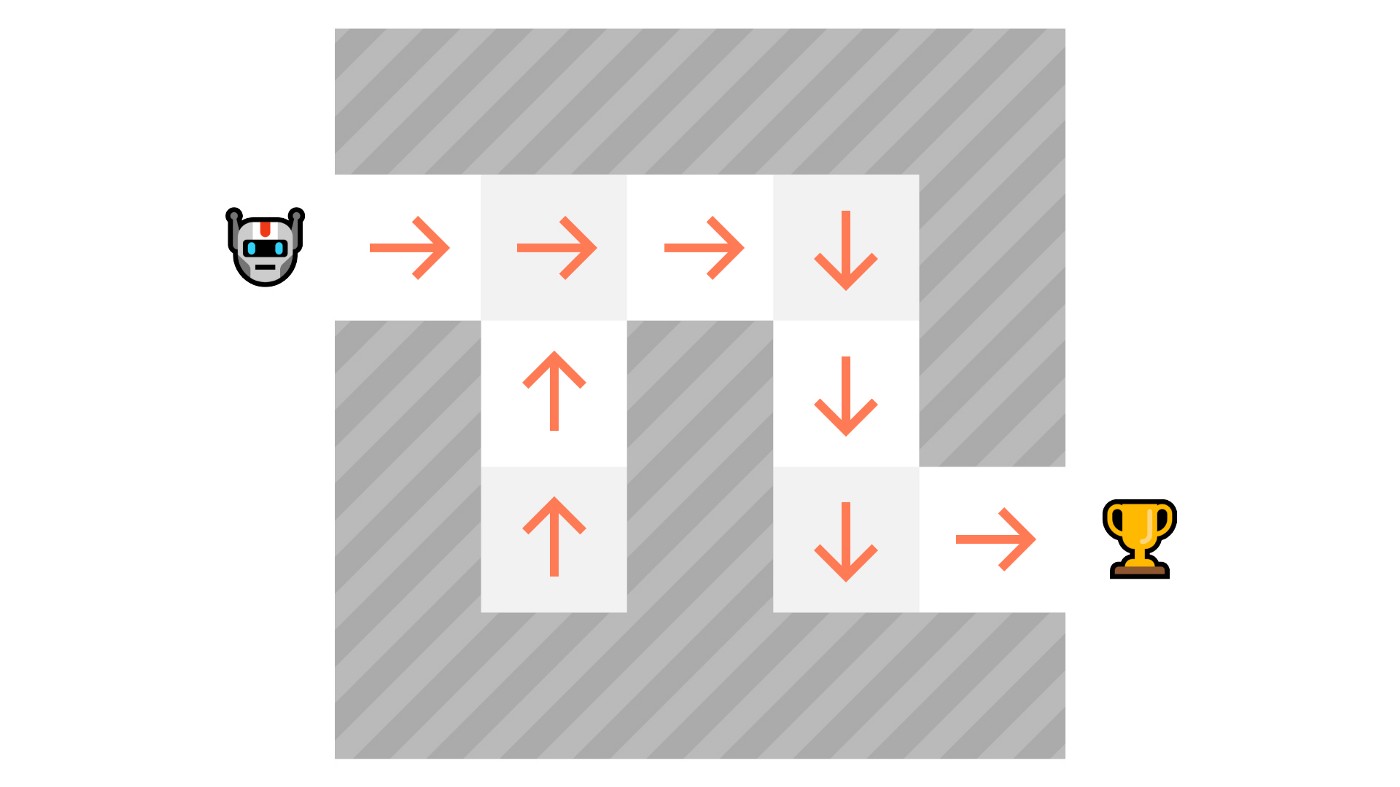
A policy can be deterministic, in which case it is usually denoted by \(\mu\):

\[a_{t} = \mu(s_{t})\]

or it may be stochastic, in which case it is usually denoted by \(\pi\):

\[a_{t}\sim\pi(\cdot|s_{t})\]

Value-based methods

In value-based methods, instead of learning a policy function, we learn the state-value function or the action-value function.

The state-value function

We write the state value function under a policy \(\pi\) like this:

\[V_{\pi}(s) = \mathbb{E}_{\pi}[G_{t}|S_{t}=s]\]

where \(G_{t} = \sum_{k=0}^{\infty}\gamma^{k}R_{t+k+1}\). For each state, the state-value function outputs the expected return if the agent starts at that state and then follows the policy forever afterward.

Here we see that our value function defined values for each possible state.

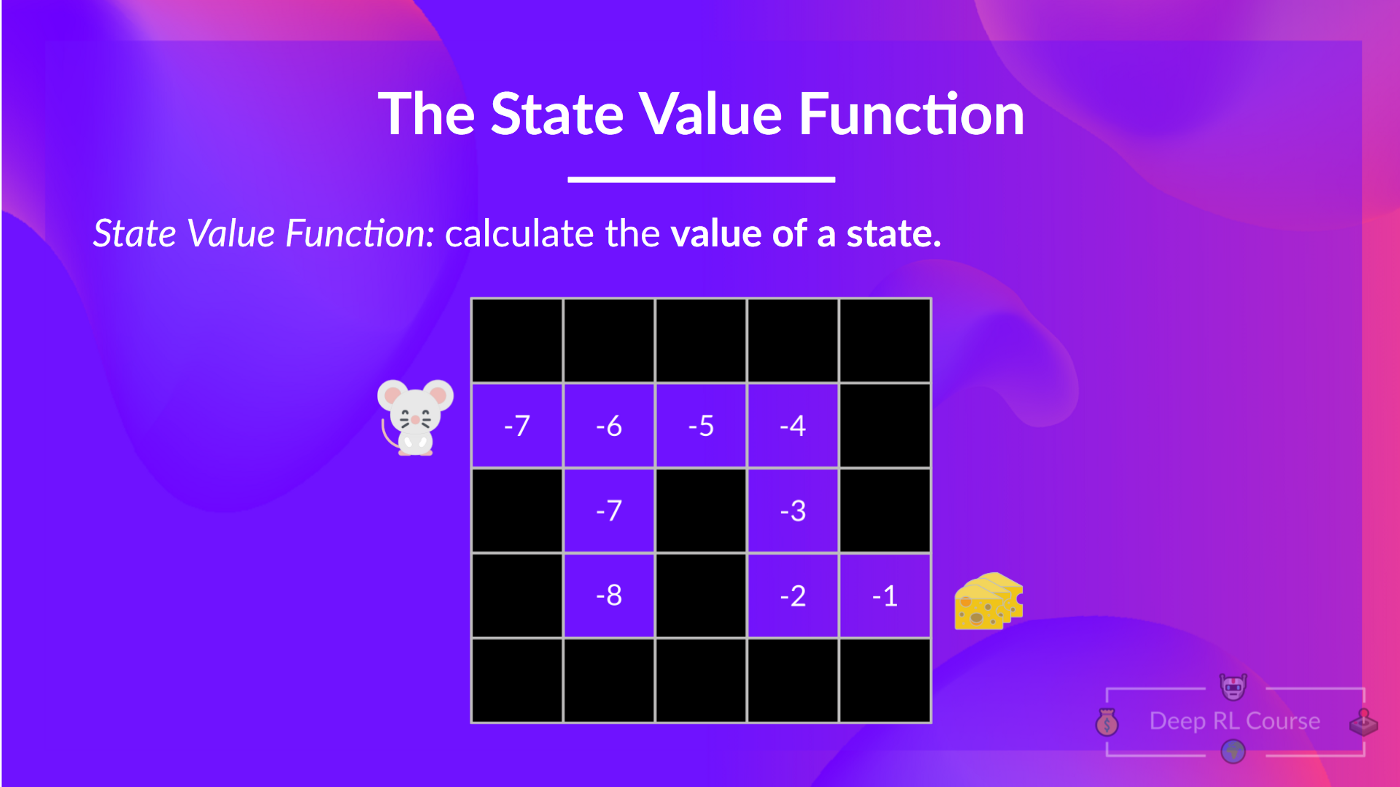
Thanks to our value function, at each step our policy will select the state with the biggest value defined by the value function: -7, then -6, then -5 (and so on) to attain the goal.

The action-value function

In the action-value function, for each state and action pair, the action-value function outputs the expected return if the agent starts in that state, takes that action, and then follows the policy forever after:

\[Q_{\pi}(s, a) = \mathbb{E}_{\pi}\left[G_{t}|S_{t}=s,A_{t}=a\right]\]

Whichever value function we choose (state-value or action-value function), the returned value is the expected return.

However, the problem is that to calculate EACH value of a state or a state-action pair, we need to sum all the rewards an agent can get if it starts at that state. This can be a computationally expensive process, and that’s where the Bellman equation comes in to help us.